ГДЗ по Алгебре за 10 класс Колягин Ю.М., Ткачева М.В. Базовый и углубленный уровень
Алгебра 10 класс Колягин Ю.М. базовый и углубленный уровень
Авторы: Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И.
«ГДЗ по алгебре за 10 класс, Базовый и углубленный уровень, Колягин (Просвещение)» было разработано лучшими педагогами страны. Авторы придерживались современной, но и не забывали о традиционной методики обучения, чтобы создать действительно полезный решебник. Школьники с любым уровнем подготовки могут использовать материалы ГДЗ для реализации собственных планов.
Алгебра в 10 классе
На предпоследней ступени изучения этого предмета учащиеся поближе познакомятся со следующими темами:
- Обратная функция.
- Длина дуги окружности.
- Синус и косинус.

- Тригонометрические функции углового аргумента и типовые задачи.
- Формулы понижения степени.
- Системы уравнений и неравенств.
На пути к получению хороших и отличных отметок будут возникать различные препятствия. Чтобы их с успехом преодолеть, необходимо заниматься не только по учебнику, но еще использовать сборник верных ответов к нему. Этих двух книг будет вполне достаточно, чтобы ученик сумел успешно освоить рабочую программу по данному предмету.
Достоинства решебника по алгебре 10 класс базовый и углубленный уровень Колягин
Одним из главных преимуществ готовых домашних заданий является то, что благодаря справочнику ученик значительно экономит время на подготовке к урокам. Свободные часы ребята могут потратить на:
- отдых;
- занятие любимым делом;
- общение с друзьями и близкими;
- подготовку к предстоящим экзаменам.
Так как старшеклассники испытывают серьезные нагрузки по всем предметам, то без надежного помощника им просто не обойтись.
Учителя и онлайн-пособие
Так как материалы «ГДЗ по алгебре за 10 класс, Базовый и углубленный уровень, Колягин Ю. М., Ткачева М. В., Федорова Н. Е., Шабунин М. И. (Просвещение)» соответствуют всем правилам и строгим требованиям Федерального компонента государственного образовательного стандарта, то пособием могут воспользоваться и преподаватели. Некоторым оно пригодится для составления поурочного и внеурочного планов. Другие могут воспользоваться решебником, чтобы сократить время проверки тетрадей учащихся с домашними заданиями. Остальные сумеют разработать собственную методику обучения. Каждый найдет в данном учебно-методическом комплексе много полезного и интересного для себя.
№ | Дата | Кол-во часов |
Тема урока | Планируемые результаты (УУД) | |||
по плану | по факту | Предметные | Метапредметные | Личностные | |||
Действительные числа (18 часов) | |||||||
1 | 02. |
| 2 | Целые и рациональные числа | Определение натуральных, целых, рациональных чисел; Определение периодической дроби. Иметь представление об иррациональных числах; множестве действительных чисел, модуле действительного числа Записывать бесконечную десятичную дробь в виде обыкновенной; выполнять действия с десятичными и обыкновенными дробями Выполнять вычисления с иррациональными выражениями, сравнивать их | Коммуникативные: развить у учащихся представление о месте математики в системе наук. Регулятивные: формировать целевые установки учебной деятельности. Познавательные: различать методы познания окружающего мира по его целям (наблюдение, опыт, эксперимент, моделирование, вычисление) | Формирование устойчивой мотивации к обучению |
2 | 02. |
| Целые и рациональные числа | ||||
3 | 04.09 |
| 2 | Действительные числа | Определение действительных чисел; Иметь представление множестве действительных чисел, модуле действительного числа Записывать бесконечную десятичную дробь в виде обыкновенной; выполнять действия действительными числами, сравнивать их. | Коммуникативные: развить у учащихся представление о месте математики в системе наук. Регулятивные: формировать целевые установки учебной деятельности. Познавательные: различать методы познания окружающего мира по его целям (наблюдение, опыт, эксперимент, моделирование, вычисление) | Формирование устойчивой мотивации к обучению |
4 | 07. |
| Действительные числа | ||||
5 | 09.09 |
| 2 | Бесконечно убывающая геометрическая прогрессия | Какая прогрессия называется геометрической; что такое бесконечно-убывающая геометрическая прогрессия; формулу суммы бесконечно убывающей геометрической прогрессии Применять формулу суммы бесконечно-убывающая геометрическая прогрессия при решении задач | Коммуникативные: определять цели и функции участников, способы взаимодействия;
планировать общие способы работы; обмениваться знаниями между членами группы
для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
6 | 09.09 |
| Бесконечно убывающая геометрическая прогрессия | ||||
7 | 11.09 |
| 4 | Определение арифметического корня натуральной степени; его свойства
| Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование устойчивой мотивации к проблемно-поисковой деятельности | |
8 | 14.09 |
| Арифметический корень натуральной степени | ||||
9 | 16.09 |
| Арифметический корень натуральной степени | Применять свойства арифметического корня натуральной степени при решении задач | Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование навыков осознанного выбора наиболее эффективного способа решения | |
10 | 16.09 |
| Арифметический корень натуральной степени | ||||
11 | 18.09 |
| 5 | Степень с рациональным и действительным показателем | Определение степе- ней с рациональным и действительным показателем; свойства степеней
| Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
12 | 21.09 |
| Степень с рациональным и действительным показателем | ||||
13 | 21.09 |
| Степень с рациональным и действительным показателем | Выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем | Регулятивные: Вносят коррективы и дополнения в способ своих действий Познавательные: Создают алгоритмы деятельности при решении проблем творческого характера Коммуникативные: Учатся контролировать, корректировать и оценивать действия партнера | Проявляют положительное отношение к урокам математики, широкий интерес к способам решения новых учебных задач, понимают причины успеха в своей учебной деятельности | |
14 | 23.09 |
| Степень с рациональным и действительным показателем | ||||
15 | 23.09 |
| Степень с рациональным и действительным показателем | ||||
16 | 25.09 |
| 2 | Урок обобщения и систематизации знаний | Определение степе- ней с рациональным и действительным показателем; свойства степеней Выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
17 | 28.09 |
| Урок обобщения и систематизации знаний | ||||
18 | 30.09 |
| 1 | Контрольная работа №1 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
Степенная функция (18 часов) | |||||||
19 | 30.09 |
| 3 | Степенная функция, её свойства и график | Свойства и графики различных случаев степенной функции
| Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
20 | 02.10 |
| Степенная функция, её свойства и график | ||||
21 | 05.10 |
| Степенная функция, её свойства и график | Сравнивать числа, решать неравенства с помощью графиков и (или) свойств степенной функции | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков осознанного выбора наиболее эффективного способа решения | |
22 | 07.10 |
| 2 | Взаимно обратные функции. Сложная функция | Определение функции обратной для данной функции, теоремы об обратной функции Строить график функции, обратной данной | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование целевых установок учебной деятельности Формирование навыков осознанного выбора наиболее эффективного способа решения |
23 | 07.10 |
| Взаимно обратные функции. Сложная функция | ||||
24 | 09.10 |
| 4 | Равносильные уравнения и неравенства | Определение равносильных уравнений, следствия уравнения; при каких преобразованиях исходное уравнение заменяется на равносильное ему уравнение, при каких получаются посторонние корни, при каких происходит потеря корней; определение равносильных неравенств
| Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
25 | 12.10 |
| Равносильные уравнения и неравенства | ||||
26 | 14.10 |
| Равносильные уравнения и неравенства | Устанавливать равносильность и следствие; выполнять необходимые преобразования при решении уравнений и неравенств | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование устойчивой мотивации к проблемно-поисковой деятельности | |
27 | 14.10 |
| Равносильные уравнения и неравенства | ||||
28 | 16.10 |
| 4 | Иррациональные уравнения | Определение иррационального уравнения; свойство Решать иррациональные уравнения | Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
29 | 19.10 |
| Иррациональные уравнения | ||||
30 | 21.10 |
| Иррациональные уравнения | Решать иррациональные уравнения | Регулятивные Вносят коррективы и дополнения в способ своих действий Познавательные Выделяют количественные характеристики объектов, заданные словами Коммуникативные Умеют с помощью вопросов добывать недостающую информацию | Проявляют мотивы учебной деятельности, дают оценку результатам своей учебной деятельности, применяют правила делового сотрудничества Объясняют свои достижения, понимают причины успеха в учебной деятельности | |
31 | 21.10 |
| Иррациональные уравнения | ||||
32 | 23.10 |
| 2 | Иррациональные неравенства | Определение иррационального неравенства; алгоритм решения этого неравенства Решать иррациональные Неравенства по алгоритму и с помощью графика | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование целевых установок учебной деятельности |
33 | 26.10 |
| Иррациональные неравенства | ||||
34 | 28.10 |
| 2 | Урок обобщения и систематизации знаний | Определение иррационального неравенства; алгоритм решения этого неравенства и уравнений Решать иррациональные Неравенства и уравнения по алгоритму и с помощью графика | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
35 | 28.10 |
| Урок обобщения и систематизации знаний | ||||
36 | 30.10 |
| 1 | Контрольная работа №2 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
Показательная функция (12 часов) | |||||||
37 | 09.11 | 2 четв | 2 | Показательная функция, её свойства и график | Определение показательной функции, три основных свойства показательной функции Строить график показательной функции | Коммуникативные: выслушивать мнение членов команды, не перебивая . Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели Познавательные: осуществлять сравнение и классификацию по заданным критериям. Уметь анализировать объекты с выделением признаков. | Формирование стартовой мотивации к изучению нового |
38 | 11.11 |
| Показательная функция, её свойства и график | ||||
39 | 11.11 |
| 3 | Показательные уравнения | Определение и вид показательных уравнений, алгоритм решения показательных уравнений
Решать показательные уравнения, пользуясь алгоритмом
| Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
40 | 13.11 |
| Показательные уравнения | ||||
41 | 16.11 |
| Показательные уравнения | ||||
42 | 18.11 |
| 3 | Показательные неравенства | Определение и вид показательных неравенств, алгоритм решения показательных уравнений Решать показательные неравенства, пользуясь алгоритмом
| Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста
| Формирование целевых установок учебной деятельности Формирование навыков анализа, сопоставления, сравнения |
43 | 18.11 |
| Показательные неравенства | ||||
44 | 20.11 |
| Показательные неравенства | ||||
45 | 23.11 |
| 2 | Системы показательных уравнений и неравенств | Способ подстановки решения систем показательных уравнений и неравенств Решать системы показательных уравнений и неравенств | Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование навыков осознанного выбора наиболее эффективного способа решения |
46 | 25.11 |
| Системы показательных уравнений и неравенств | ||||
47 | 25.11 |
| 1 | Урок обобщения и систематизации знаний | Способ подстановки решения систем показательных уравнений и неравенств Решать системы показательных уравнений и неравенств | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
48 | 27.11 |
|
| Контрольная работа №3 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
Логарифмическая функция (19 часов) | |||||||
49 | 30.11 |
| 2 | Логарифмы | Определение логарифма числа, основное логарифмическое тождество Выполнять преобразование выражений, содержащих логарифмы | Коммуникативные: выслушивать мнение членов команды, не перебивая . Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели Познавательные: осуществлять сравнение и классификацию по заданным критериям. Уметь анализировать объекты с выделением признаков. | Формирование стартовой мотивации к изучению нового |
50 | 02.12 |
| Логарифмы | ||||
51 | 02.12 |
| 2 | Свойства логарифмов | Свойства логарифмов Применять свойства логарифмов при преобразовании выражений, содержащих логарифмы | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование целевых установок учебной деятельности |
52 | 04.12 |
| Свойства логарифмов | ||||
53 | 07.12 |
| 3 | Десятичные и натуральные логарифмы. Формула перехода | Обозначение десятичного и натурального логарифма; ознакомиться с таблицей Брадиса
| Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование целевых установок учебной деятельности |
54 | 09.12 |
| Десятичные и натуральные логарифмы. Формула перехода | ||||
55 | 09.12 |
| Десятичные и натуральные логарифмы. Формула перехода | Находить значения десятичных и натуральных логарифмов по таблицам Брадиса и с помощью МК
| Регулятивные: Осознают качество и уровень усвоения Познавательные: Выбирают наиболее эффективные способы решения задачи Коммуникативные: Регулируют собственную деятельность посредством письменной речи | Формирование у учащихся умения к осуществлению контрольной функции, контроль и самоконтроль изученных знаний (выполнение контрольной работы) | |
56 | 11.12 |
| 2 | Логарифмическая функция, её свойства и график | Вид логарифмической функции, её основные свойства Строить график логарифмической функции с данным основанием, использовать свойства логарифмической функции при решении задач | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
57 | 14.12 |
| Логарифмическая функция, её свойства и график | ||||
58 | 16.12 |
| 3 | Логарифмические уравнения | Вид простейших логарифмических уравнений, основные приёмы решения логарифмических уравнений
| Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста
| Формирование целевых установок учебной деятельности Формирование навыков анализа, сопоставления, сравнения |
59 | 16.12 |
| Логарифмические уравнения | ||||
60 | 18.12 |
| Логарифмические уравнения | Решать простейшие логарифмические уравнения и применять основные приёмы при решении уравнений | Регулятивные: Самостоятельно составляют алгоритм деятельности при решении учебной задачи Познавательные: Устанавливают аналогии для понимания закономерностей, используют их при решении задач Коммуникативные: Проектируют и формируют учебное сотрудничество с учителем и сверстниками | Осознают роль ученика, осваивают личностный смысл учения | |
61 | 21.12 |
| 4 | Логарифмические неравенства | Вид простейших логарифмических неравенств, основные приёмы решения логарифмических неравенств
| Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
62 | 23.12 |
| Логарифмические неравенства | ||||
63 | 23.12 |
| Логарифмические неравенства | Решать простейшие логарифмические неравенства и применять основные приёмы при решении неравенств | Познавательные: Осуществляют сравнение, извлекают необходимую информацию, переформулируют условие, строят логическую цепочку Регулятивные: Работая по плану, сверяют свои действия с целью, вносят корректировки Коммуникативные: Сотрудничают с одноклассниками при решении задач; умеют выслушать оппонента. Формулируют выводы | Проявляют познавательную активность, творчество | |
64 | 25.12 |
| Логарифмические неравенства | ||||
65 | 11.01 | 3 четв |
| Урок обобщения и систематизации знаний | Вид простейших логарифмических неравенств, основные приёмы решения логарифмических неравенств и уравнений Решать простейшие логарифмические неравенства и применять основные приёмы при решении неравенств и уравнений | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
66 | 13.01 |
|
| Урок обобщения и систематизации знаний | |||
67 | 13.01 |
|
| Контрольная работа №4 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
Тригонометрические формулы (27 часов) | |||||||
68 | 15.01 |
| 1 | Радианная мера угла | Определение угла в один радиан, формулы перевода градусной меры в радианную и наоборот Пользоваться формулами перевода, вычислять длину дуги и площадь кругового сектора | Коммуникативные: выслушивать мнение членов команды, не перебивая . Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели Познавательные: осуществлять сравнение и классификацию по заданным критериям. Уметь анализировать объекты с выделением признаков. | Формирование стартовой мотивации к изучению нового |
69 | 18.01 |
| 2 | Поворот точки вокруг начала координат | Понятие «единичная окружность», поворот точки вокруг начала координат Находить координаты точки единичной окружности, полученной поворотом P(1;0) На заданный угол, находить углы поворота точки P(1;0), чтобы получить точку с заданными координатами | Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
70 | 20.01 |
| Поворот точки вокруг начала координат | ||||
71 | 20.01 |
| 2 | Определение синуса, косинуса и тангенса угла | Определение синуса, косинуса и тангенса угла Находить значения синуса, косинуса и тангенса угла по таблицам Брадиса и с помощью МК; табличные значения; решать уравнения sin x=0, sin x=1, sin x=-1, cos x=0, cos x=1, cos x=-1 | Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
72 | 22.01 |
| Определение синуса, косинуса и тангенса угла | ||||
73 | 25.01 |
| 1 | Знаки синуса, косинуса и тангенса угла | Основное тригонометрическое тождество, зависимость между тангенсом и котангенсом, зависимость между тангенсом и косинусом, зависимость между котангенсом и синусом Применять формулы зависимости между синусом, косинусом и тангенсом одного и того же угла при решении задач | Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
74 | 27.01 |
| 2 | Зависимость между синусом, косинусом и тангенсом одного и того же угла | Основное тригонометрическое тождество, зависимость между тангенсом и котангенсом, зависимость между тангенсом и косинусом, зависимость между котангенсом и синусом Применять формулы зависимости между синусом, косинусом и тангенсом одного и того же угла при решении задач | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков анализа, сопоставления, сравнения |
75 | 27.01 |
| Зависимость между синусом, косинусом и тангенсом одного и того же угла | ||||
76 | 29.01 |
| 3 | Тригонометрические тождества | Какие равенства называются тождествами, какие способы используются при доказательстве тождеств
| Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные : оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
77 | 01.02 |
| Тригонометрические тождества | ||||
78 | 03.02 |
| Тригонометрические тождества | Применять изученные формулы при доказательстве тождеств | Регулятивные: Работают по плану, сверяясь с целью, корректируют план Познавательные: Структурируют знания, определяют основную и второстепенную информацию Коммуникативные: Приводят аргументы в пользу своей точки зрения, подтверждают ее фактами | Осваивают культуру работы с учебником, поиска информации | |
79 | 03.02 |
| 1 | Синус, косинус и тангенс углов α и — α | Формулы sin(-a)= — sina, cos(-a)=cos, tg(-a)=-tg a Находить значения синуса, косинуса и тангенса для отрицательных углов | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков анализа, сопоставления, сравнения |
80 | 05.02 |
| 3 | Формулы сложения | Формулы сложения сos(a+b) и другие
| Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
81 | 08.02 |
| Формулы сложения | ||||
82 | 10.02 |
| Формулы сложения | Выводить формулы сложения и применять их на практике | Регулятивные: Самостоятельно составляют алгоритм деятельности при решении учебной задачи Познавательные: Устанавливают аналогии для понимания закономерностей, используют их при решении задач Коммуникативные: Сотрудничают с одноклассниками при решении задач; умеют выслушать оппонента. | Грамотно и аргументировано излагают свои мысли, проявляют уважительное отношение к мнениям других людей
| |
83 | 10.02 |
| 2 | Синус, косинус и тангенс двойного угла | Формулы синуса, косинуса и тангенса двойного угла Выводить формулы двойного угла и применять их на практике | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков анализа, сопоставления, сравнения |
84 | 12.02 |
| Синус, косинус и тангенс двойного угла | ||||
85 | 15.02 |
| 2 | Синус, косинус и тангенс половинного угла | Формулы половинного угла синуса, косинуса и тангенса; Формулы, выражающие sina, cosa и tg a через tg (a/2) Выводить формулы половинного угла синуса, косинуса и тангенса; применять их на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
86 | 17.02 |
| Синус, косинус и тангенс половинного угла | ||||
87 | 17.02 |
| 2 | Формулы привидения | Значения тригонометрических функций углов, больших 90°, сводятся к значениям для острых углов; правила записи формул приведения Применять формулы приведения при решении задач | Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков анализа, сопоставления, сравнения |
88 | 19.02 |
| Формулы привидения | ||||
89 | 24.02 |
| 3 | Сумма и разность синусов. Сумма и разность косинусов | Формулы суммы и разности синусов, суммы и разности косинусов
| Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков анализа, сопоставления, сравнения |
90 | 24.02 |
| Сумма и разность синусов. Сумма и разность косинусов | ||||
91 | 26.02 |
| Сумма и разность синусов. Сумма и разность косинусов | Применять формулы суммы и разности синусов, суммы и разности косинусов на практике | Регулятивные: Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению Познавательные: Осуществляют сравнение, извлекают необходимую информацию, переформулируют условие, строят логическую цепочку Коммуникативные: Формулируют собственное мнение и позицию, задают вопросы, слушают собеседника | Осознают роль ученика, осваивают личностный смысл учения | |
92 | 01.03 |
| 2 | Урок обобщения и систематизации знаний | Формулы суммы и разности синусов, суммы и разности косинусов Применять формулы суммы и разности синусов, суммы и разности косинусов на практике | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
93 | 03.03 |
| Урок обобщения и систематизации знаний | ||||
94 | 03.03 |
|
| Контрольная работа №5 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
Тригонометрические уравнения (18 часов) | |||||||
95 | 05.03 |
| 3 | Уравнение | Определение арккосинуса числа, формулу решения уравнения cos х=а, частные случаи решения уравнения (cos х=1, cos х=-1, cos х=0) Решать простейшие тригонометрические уравнения вида cos х=а | Коммуникативные: выслушивать мнение членов команды, не перебивая . Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели Познавательные: осуществлять сравнение и классификацию по заданным критериям. Уметь анализировать объекты с выделением признаков. | Формирование стартовой мотивации к изучению нового |
96 | 05.03 |
| Уравнение | ||||
97 | 10.03 |
| Уравнение | Решать простейшие тригонометрические уравнения вида cos х=а | Познавательные: Осуществляют сравнение, извлекают необходимую информацию, переформулируют условие, строят логическую цепочку Регулятивные: Работая по плану, сверяют свои действия с целью, вносят корректировки Коммуникативные: Сотрудничают с одноклассниками при решении задач; умеют выслушать оппонента. Формулируют выводы | Проявляют познавательную активность, творчество | |
98 | 10.03 |
| 3 | Уравнение | Определение арксинуса числа, формулу решения уравнения sin х=а, частные случаи решения уравнения (sin х=1, sin х=-1, sin х=0)
| Коммуникативные: проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции Регулятивные: осознавать качество и уровень усвоения Познавательные: создавать структуру взаимосвязей смысловых единиц текста | Формирование навыков анализа, сопоставления, сравнения |
99 | 12.03 |
| Уравнение | ||||
100 | 15.03 |
| Уравнение | Решать простейшие тригонометрические уравнения вида sin х=а | Познавательные: Осуществляют сравнение, извлекают необходимую информацию, переформулируют условие, строят логическую цепочку Регулятивные: Работая по плану, сверяют свои действия с целью, вносят корректировки Коммуникативные: Сотрудничают с одноклассниками при решении задач; умеют выслушать оппонента. Формулируют выводы | Проявляют познавательную активность, творчество | |
101 | 17.03 |
| 2 | Уравнение | Определение арктангенса числа, формулу решения уравнения tg х=а Применять формулу решения уравнения tg х=а для решения уравнений | Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
102 | 17.03 |
| Уравнение | ||||
103 | 19.03 |
| 5 | Решение тригонометрических уравнений | Некоторые виды тригонометрических уравнений | Коммуникативные: способствовать формированию научного мировоззрения. Регулятивные: оценивать весомость приводимых доказательств и рассуждений. Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
104 | 29.03 | 4 четв | Решение тригонометрических уравнений | Решать простейшие тригонометрические уравнения
| Регулятивные: Выделяют и осознают то, что уже усвоено и что еще подлежит усвоению Познавательные: Осуществляют сравнение, извлекают необходимую информацию, переформулируют условие, строят логическую цепочку Коммуникативные: Формулируют собственное мнение и позицию, задают вопросы, слушают собеседника | Осознают роль ученика, осваивают личностный смысл учения | |
105 | 31.03 |
| Решение тригонометрических уравнений | ||||
106 | 31.03 |
| Решение тригонометрических уравнений | Решать квадратные уравнения относительно одной из тригонометрических функций, однородные и не однородные уравнения | Регулятивные: Работают по плану, сверяясь с целью, корректируют план Познавательные: Структурируют знания, определяют основную и второстепенную информацию Коммуникативные: Приводят аргументы в пользу своей точки зрения, подтверждают ее фактами | Осваивают культуру работы с учебником, поиска информации | |
107 | 02.04 |
| Решение тригонометрических уравнений | ||||
108 | 05.04 |
| 2 | Примеры решения простейших тригонометрических неравенств | Алгоритм решения простейших тригонометрических неравенств Решать простейшие тригонометрические неравенства | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
109 | 07.04 |
| Примеры решения простейших тригонометрических неравенств | ||||
110 | 07.04 |
|
| Урок обобщения и систематизации знаний | Алгоритм решения простейших тригонометрических неравенств и уравнений Решать простейшие тригонометрические Неравенства и уравнения | Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками. Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий. Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию. | Формирование навыков организации и анализа своей деятельности, самоанализа и самокоррекции учебной деятельности |
111 | 09.04 |
|
| Урок обобщения и систематизации знаний | |||
112 | 12.04 |
|
| Контрольная работа №6 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
Итоговое повторение (24 часа) | |||||||
113 | 14.04 |
| 3 | Действительные числа.
| См тему «Действительные числа»
| Коммуникативные: выслушивать мнение членов команды, не перебивая . Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели Познавательные: осуществлять сравнение и классификацию по заданным критериям. Уметь анализировать объекты с выделением признаков. | Формирование стартовой мотивации к изучению нового |
114 | 14.04 |
| Действительные числа.
| ||||
115 | 16.04 |
| Действительные числа.
| ||||
116 | 19.04 |
| 3 | Степенная функция.
| См тему «Степенная функция»
| Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
117 | 21.04 |
| Степенная функция.
| ||||
118 | 21.04 |
| Степенная функция.
| ||||
119 | 23.04 |
| 4 | Показательная функция
| См. тему «Показательная функция» | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
120 | 26.04 |
| Показательная функция
| ||||
121 | 28.04 |
| Показательная функция
| ||||
122 | 28.04 |
| Показательная функция | ||||
123 | 30.04 |
| 3 | Логарифмическая функция. | См. тему «Логарифмическая функция»
| Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
124 | 04.05 |
| Логарифмическая функция. | ||||
125 | 05.05 |
| Логарифмическая функция. | ||||
126 | 05.05 |
| 4 | Тригонометрические формулы и уравнения. | См. тему «Тригонометрия»
| Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
127 | 07.05 |
| Тригонометрические формулы и уравнения. | ||||
128 | 11.05 |
| Тригонометрические формулы и уравнения. | ||||
129 | 12.05 |
| Тригонометрические формулы и уравнения | ||||
130 | 12.05 |
|
| Итоговая контрольная работа №7 | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
131 | 14.05 |
| 4 | Решение вариантов ЕГЭ | Научиться применять теоретический материал, изученный на предыдущих уроках, на практике | Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
132 | 17.05 |
| Решение вариантов ЕГЭ | ||||
133 | 19.05 |
| Решение вариантов ЕГЭ | ||||
134 | 19.05 |
| Решение вариантов ЕГЭ | ||||
135 | 21.05 |
| 2 | Урок обобщения и систематизации знаний | Повторить теоретический материал, изученный на предыдущих уроках, закрепить умение применять полученные знания на практике | Коммуникативные: регулировать собственную деятельность посредством письменной речи Регулятивные: оценивать достигнутый результат Познавательные: выбирать наиболее эффективные способы решения задачи | Формирование навыка самоанализа и самоконтроля |
136 | 24.05 |
| Урок обобщения и систематизации знаний | ||||
Алгебра и начала математического анализа. 10 класс (профильный уровень) Колягин Ю.М. и др.
Учебник Ю.М.Колягина «Алгебра и начала анализа.10 класс» полностью соответствует программе Ш.А.Алимова для старших классов и является органичным продолжением учебников алгебры для 7-9 классов, подготовленных авторским коллективом в составе: Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. («Просвещение»). Это обеспечивает его использование при изучении алгебры в общеобразовательных школах.Отличительной особенностью учебника является то, что отвечая требованиям реформирования общего и среднего образования, они позволяют организовать как профильную, так и уровневую дифференциацию обучения в старших классах. Традиционный программный материал курса дополнен углублением теоретических сведений, демонстрацией прикладных аспектов вводимых понятий, историческими очерками. В учебнике представлен в целостном виде раздел по тригонометрии. Широко представлены разные типы тригонометрических уравнений и методы их решения. Много внимания уделяется алгебраическим, показательным и логарифмическим примерам и задачам. Содержит избыточную и разделенную по трем уровням сложности систему задач и упражнений. Дополнительно разбираются задачи вступительных экзаменов в различные вузы.
ОГЛАВЛЕНИЕ
Предисловие 3
Глава I. Действительные числа. Степень с действительным показателем
§ 1. Рациональные числа 5
§ 2. Бесконечно убывающая геометрическая прогрессия 8
§ 3. Действительные числа 15
§ 4. Арифметический корень натуральной степени 18
§ 5. Степень с рациональным показателем 25
§ 6. Степень с действительным показателем 32
Упражнения к главе I 36
Историческая справка 40
Глава II. Показательная функция
§ 7. Показательная функция, ее свойства и график 43
§ 8. Показательные уравнения и неравенства 51
Упражнения к главе II 56
Историческая справка 59
Глава III. Степенная функция
§ 9. Степенная функция, ее свойства и график 60
§ 10. Взаимно обратные функции 66
§ 11. Равносильные уравнения и неравенства 71
§ 12. Иррациональные уравнения 77
§ 13. Иррациональные неравенства 81
Упражнения к главе III 88
Историческая справка 91
Глава IV. Логарифмическая функция
§ 14. Логарифмы 92
§ 15. Свойства логарифмов 96
§ 16. Десятичные и натуральные логарифмы. Формула перехода 100
§ 17. Логарифмическая функция, ее свойства и график 105
§ 18. Логарифмические уравнения 111
§ 19. Логарифмические неравенства 117
Упражнения к главе IV 123
Историческая справка 128
Глава V. Системы уравнений
§ 20. Способ подстановки 131
§ 21. Способ сложения 136
§ 22. Решение систем уравнений различными способами 141
§ 23. Решение задач с помощью систем уравнений 154
Упражнения к главе V 160
Историческая справка 164
Глава VI. Тригонометрические формулы
§ 24. Радианная мера угла 165
§ 25. Поворот точки вокруг начала координат 168
§ 26. Определение синуса, косинуса и тангенса угла 174
§ 27. Знаки синуса, косинуса и тангенса угла 180
§ 28. Зависимость между синусом, косинусом и тангенсом одного и того же угла 184
§ 29. Тригонометрические тождества 188
§ 30. Синус, косинус, танген
Гдз по алгебре 10 колягин ткачева федорова
Колягин ю м ткачева алгебра 10 класс гдз. Решебник (ГДЗ) для 10‐11 класса по алгебре. Авторы учебника: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачёва Содержит в себе полные и подробные ответы на все упражнения онлайн на пять ру. Гдз по алгебре 10 класс колягин ткачева шабунин. Р. Р. Просто зайдите на страницу гдз алгебра 10-11 класс Алимов, Н. Учебник А. Колягин, Ю. Сидоров, М. Ткачева, Н. Столбов, А. Шабунин. Помогите найти ГДЗ. Учебника 10 класс Алгебра и начала анализа Колягин, дз по алгебре 10 класс колягин. Пользователь андрей лапаев задал вопрос в категории Домашние задания и получил на него 1 ответ. Приветствуем на образовательном портале Еуроки. Здесь вы найдете ГДЗ с подробным и полным решением упражнений колягин по Алгебре базовый понятие и значение договора страхования шпаргалка углублённый уровни за 10 класс, автор: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Издательство: Просвещение ФГОС. Vklasse.org — это портал, на котором ты сможешь найти учебники и решебники (ГДЗ) по всем предметам школьной программы для разных классов. Портал полностью адаптирован под твой смартфон. ГДЗ: Спиши готовые алгебры задания базовый и углублённый уровни по алгебре за 10 класс, решебник Колягин Ю.М., ФГОС, онлайн ответы на GDZ. ГДЗ по алгебре авторами которого являются Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Мегаботан — подробные гдз базовый и углублённый уровни алгебра Алгебре для 10 класса, авторов: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Полный и ткачева решебник (ГДЗ) Алгебра 10 класс Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева 2012. Доступно гдз ваших смартфонах. Подробные решебник и гдз к учебнику алгебры 10-11 класс, авторов Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачёва на 2015 — 2016 учебный год. Авторы: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. В учебнике по алгебре 10 класса Колягина отдельно выделяется материал для изучения математического анализа. Упражнения раздельно колягин как для базового и профильного уровней, так и для интересующихся математикой. ГДЗ по алгебре за 10 класс Колягин, Ткачева, Федорова, Шабунин позволяет школьникам освоить базовый и углубленный уровень самостоятельно. Решебник предоставляет ответы к номеру и на вопросы из учебника алгебра и начала математического анализа за 10 класс. Онлайн решебник базовый и ткачева уровни по Алгебре для 10 класса Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И., гдз и классы к домашнему заданию. Решебник и ГДЗ по Алгебре для 10 класса базовый и углублённый уровни, авторы учебника: Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. на 2017-2018 год.
Гдз русский 9 класс тростенцова 2016
Гдз ладыженская 9 класс 2016
ГДЗ Алгебра 10 класс Колягин, Ткачёва, Фёдорова, Шабунин
Алгебра 10 класс
Учебник (Базовый и углубленный уровень)
Колягин, Ткачёва, Фёдорова, Шабунин
Просвещение
Данный предмет редко у кого вызывает положительные эмоции, ведь чтобы правильно написать хоть одно уравнение необходимо хорошо знать теорию. Причем не только ту, что проходится на данном этапе, но и всю, что изучалась до этого. Так как в данной науке все взаимосвязано, то очень важно помнить обо всех этих нюансах. Кроме того, это поможет легче воспринимать материал и не испытывать дефицит с информацией. Преодолевать возникающие затруднения поможет решебник к учебнику «Алгебра и начала математического анализа 10 класс» Колягин, Ткачева, Федорова.
Основные параметры издания
В пособии содержится более тысячи двухсот упражнений, а так же вопросы к параграфам и задания для самопроверки. Авторы подробно разобрали каждый номер и предоставили полноценные исчерпывающие решения, которые помогут лучше справиться с подготовкой д/з. ГДЗ по алгебре 10 класс Колягин поспособствует так же более полному усвоению текущего материала.
Каким целям отвечает его использование
Программа по алгебре в десятом классе весьма сложна и требует не просто внимательного подхода, но и крайней сосредоточенности. Подростки же склонны отвлекаться во время уроков и это при том, что подача информации со стороны учителя и так ведется в крайне скудной манере. Кроме того, редко у кого из школьников есть привычка изучать пройденный на уроке параграф, чтобы лучше понять тему. В основном они все оставляют на потом, а задания стараются либо списывать, либо делают их крайне поверхностно. Пользы это не приносит никакой, зато успеваемость снизить может. Ведь смысл решебника к учебнику «Алгебра и начала математического анализа 10 класс (базовый и углубленный уровень)» Колягин состоит в том, что каждое упражнение должно тщательно исследоваться, а не просто переписываться. «Просвещение», 2017 г.
Алимов колягин сидоров 10 11.
3-е изд. — М .: Просвещение, 2016. — 464 с.
Учебник завершает разработку основных идей курса алгебры в 7-9 классах авторов Ш.А. Алимов и другие. Элементарные функции изучаются в 10 классе классическими элементарными методами без привлечения производной; числовая линия и линия преобразований развиваются параллельно с функционалом; Начала математического анализа рассматриваются в 11 классе.Система упражнений представлена на трех уровнях сложности. Задачи повышенной сложности в конце учебника содержат богатый материал для подготовки к вузам с повышенными требованиями по математике.
2016 , 3 изд., 464с.)
Формат: pdf
Размер: 9,1 МБ
Watch, скачать: ноябрь
Алгебра и начало математического анализа. ( 2012 г. , 18 изд., 464с.)
Формат: pdf
Размер: 42,7 МБ
Смотреть, скачать: ноябрь .2019, ссылки удалены по просьбе издательства «Образование» (см. Примечание)
Алгебра и начало анализа. ( 2007 г. , 15 изд., 384с.)
Формат: pdf
Размер: 10,3 МБ
Часы, скачать: ноябрь .2019, ссылки удалены по просьбе издательства «Образование» (см. Примечание)
СОДЕРЖАНИЕ
Глава 1.Действительные числа
§ 1. Целые и рациональные числа 3
§ 2. Действительные числа 7
§ 3. Бесконечно убывающая геометрическая прогрессия. … одиннадцать
§ 4. Арифметический корень натуральной степени 17
§ 5. Степень с рациональными и действительными показателями 24
Упражнения для главы I 35
Глава II. Степенные функции
§ 6. Степенная функция, ее свойства и график 39
§ 7. Взаимно обратные функции 47
§ 8. Эквивалентные уравнения и неравенства 54
§ 9.Иррациональные уравнения 60
§ десять *. Иррациональные неравенства 63
Упражнения к главе II 69
Глава III. Экспоненциальная функция
§ одиннадцать. Экспоненциальная функция, ее свойства и график 72
§ 12. Экспоненциальные уравнения 77
§ 13. Экспоненциальные неравенства 81
§ 14. Системы экспоненциальных уравнений и неравенств … 84
Упражнения к главе III 87
Глава IV. .Логарифмическая функция
§ 15. Логарифмы 90
§ 16.Свойства логарифмов 94
§ 17. Десятичные и натуральные логарифмы 96
§ 18. Логарифмическая функция, ее свойства и график. … 100
§ 19. Логарифмические уравнения 105
§ 20. Логарифмические неравенства 109
Упражнения для главы IV 113
Глава V. Тригонометрические формулы
§ 21. Радианная мера угла 117
§ 22. Вращение точки вокруг начало координат 121
§ 23. Определение синуса, косинуса и тангенса угла …. 126
§ 24. Знаки синуса, косинуса и тангенса 132
§ 25. Зависимость между синусом, косинусом и тангенсом одного и того же угла 135
§ 26. Тригонометрические тождества 139
§ 27. Синус, косинус и тангенс его углов и — a 142
§ 28. Формулы сложения 144
§ 29. Синус, косинус и тангенс двойного угла 149
§ тридцать *. Синус, косинус и полуугол 152
§ 31. Формулы приведения 156
§ 32. Сумма и разность синусов. Сумма и разность косинусов 161
Упражнения к главе V 164
Глава VI.Тригонометрические уравнения
§ 33. Уравнение cos x = a 168
§ 34. Уравнение sin x = a 173
§ 35. Уравнение tan x = a 179
§ 36. Решение тригонометрических уравнений 184
§ 37 *. Примеры решения простейших тригонометрических неравенств 194
Упражнения к главе VI 197
Глава VII. Тригонометрические функции
§ 38. Область и множество значений тригонометрических функций 201
§ 39. Четность, нечетность, периодичность тригонометрических функций 204
§ 40.Свойства функции y = cos x и ее графика 208
§ 41. Свойства функции y = sin x и ее графика 213
§ 42. Свойства функции y = tg x и ее графика 217
Раздел 43 *. Обратные тригонометрические функции 223
Упражнения для главы VII 227
Глава VIII. Производная и ее геометрическое значение
§ 44. Производная 229
§ 45. Производная степенной функции 236
Раздел 46. Правила дифференцирования 240
§ 47. Производные некоторых элементарных функций…. … 245
§ 48. Геометрическое значение производной 251
Упражнения к главе VIII 257
Глава IX. Применение производной к изучению функций
§ 49. Увеличение и уменьшение функции 261
§ 50. Экстремумы функции 265
§ 51. Применение производной к построению графиков функций 271
§ 52. Наибольшее и наименьшее значение функции …. 277
§ 53 *. Выпуклость графика функции, точки перегиба… 283
Глава IX Упражнения 287
Глава X. Интеграл
§ 54. Первообразное 291
Раздел 55. Правила поиска первообразных 294
§ 56. Площадь криволинейной трапеции и интеграла …. 297
§ 57. Вычисление интегралов 301
§ 58. Вычисление площадей с помощью интегралов …. 304
§ 59 *. Применение производной и интеграла к решению практических задач 309
Упражнения к главе X 315
Добавлено в новой редакции.
Глава XI Комбинаторика
Раздел 60. Правило произведения 317
Раздел 61. Перестановки 320
§ 62. Размещение 323
Раздел 63. Комбинации и их свойства 326
§ 64. Бином Ньютона 330
Упражнения для главы XI 333
Глава XII. Элементы теории вероятностей
Раздел 65. События 336
Раздел 66. Комбинации событий. Обратное событие. … 339
Статья 67. Вероятность события 343
Статья 68.Сложение вероятностей 346
Раздел 69. Независимые события. Умножение вероятностей. … … 350
Раздел 70. Статистическая вероятность 354
Упражнения для главы XII 359
Глава XIII. Статистика
§ 71. Случайные переменные 364
Раздел 72. Центральные тенденции 370
§ 73. Меры дисперсии 375
Упражнения для Главы XIII 383
Приложение
§ 1. Наборы 387
§ 2. Элементы математической логики 388
§ 3.Предел последовательности 390
§ 4. Дробно-линейная функция и ее график 393
§ 5. Уравнения и неравенства с двумя неизвестными. … … 395
Упражнения для окончательного повторения курса алгебры и начала математического анализа. … … … 400
Задания для внеклассных занятий 426
Ответы и направления 432
Указатель 460
10-11 класс по алгебре
Алимов, Колягин, Сидоров
Образование
Это было начало самого тяжелого периода в школьной жизни подростков.На горизонте маячит нелюбимая многими НГЭ, так что расслабляться ни в коем случае не стоит. Более того, в этот период начинается знакомство с высшей математикой, которую не так легко понять, как обычную алгебру. Решебник для учебника «Алгебра 10-11 класс» Алимов, Колягин, Сидоров всегда придет на помощь в сложных ситуациях, особенно когда подросток не получает всю информацию на уроках.
Что входит в комплект.
В пособии подробно проанализирован каждый аспект учебника, чтобы школьники могли найти и повторить любую тему в любое время, а также освежить в памяти уже пройденные этапы.Тщательность решений в ГДЗ в 10-11 классах алгебры способствует тому, что даже малейшие нюансы не ускользнут от внимания подростков, и эта тема больше не будет казаться такой устрашающей.
Нужен ли мне резольвер.
Многие тесты уже пройдены, но впереди их еще много. Поэтому будет крайне обидно, если именно в этот период резко упадет успеваемость. А поскольку остальным школьникам предстоит проходить ОГЭ, это совсем не желательно.Но для того, чтобы достойно пройти все препятствия, потребуется не только внимательность к урокам, но и хорошее понимание материала. Для этого решебник как нельзя лучше подходит к учебнику. «Алгебра 10-11 классы» Алимова , потому что именно в этом пособии подростки смогут найти все необходимое для успешной учебы.
«Образование», 2012
Обучение в современной школе требует от ученика много времени и сил. Особенно, если речь идет об изучении математических дисциплин, в том числе и алгебры.
Многие учителя не успевают эффективно контролировать уровень знаний учащихся. Домашнее задание оценивается схематично, и на первом месте стоит не формирование живого интереса к обучению и получению знаний, а отчет о результатах успеваемости.
В этой ситуации ученики, от которых родители также требуют хорошей успеваемости, не находят ничего лучшего, как списать выполненные домашние задания с решебников. Фактически это приводит только к тому, что ребенок перестает понимать предмет.Чтобы ГДЗ приносили реальную пользу, необходимо методично их правильно использовать.
Как правильно использовать решение Алимова по алгебре 10-11 классов
Все ответы на домашние задания составляются тем же авторским коллективом, который создавал сам учебник. ГДЗ — это не просто возможность безрадостно списать безнадзорному школьнику, это, прежде всего, учебно-методическое пособие, которое должно улучшить дидактическую составляющую учебного процесса.
- Важно помнить, что домашнее задание — это не только примеры, но и теоретический материал, без усвоения которого невозможно успешно справиться.
- Готовые ответы следует использовать не для накрутки, а только для того, чтобы проверить правильность заданий.
- Решения для того или иного примера основаны на той или иной теме тренинга, в инструкции есть ссылки на нее. Поэтому, если ученик испытывает затруднения, то в этом случае необходимо вернуться к предыдущему материалу и повторить его заново.Все это позволяет превратить решебник в эффективное средство контроля успеваемости, а также помочь студентам развить стимул к самостоятельному обучению.
Найди все ответы по алгебре для 10-11 классов Алимова онлайн
Мы стремимся сделать обучение более полным и эффективным. Для этого на нашем сайте размещены учебники, а также ГДЗ по различным школьным дисциплинам.
Теперь вам не нужно покупать пачку бумажных руководств. Все доступно в электронном виде в любое время.Вы можете посетить наш сайт с ПК, смартфона или планшета. Это очень удобно, так как позволяет получать ответы на задания даже в общественном транспорте или в другом месте.
Старшеклассники никогда не знают, в какой момент у них могут возникнуть проблемы с учебой. Любой предмет, изучаемый в школе, может доставить трудности, от русского языка до безопасности жизни. Алгебра — одна из академических дисциплин, от которой у студентов регулярно появляется потливость. Алгебраика начинает терроризировать умы детей с седьмого класса и продолжает это дело на десятом и одиннадцатом годах обучения.Подростки могут облегчить себе жизнь разными способами, в том числе решебниками.
Сборник ГДЗ для 10-11 классов по алгебре (Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева) Прекрасное дополнение к основной книге. С помощью предоставленной в нем помощи ученик готов решать любое упражнение. Задания предполагают анализ следующих тем:
- тригонометрические функции и уравнения;
- логарифмов;
- градусов.
В представленных ответах и комментариях есть необходимые авторские пометки, которые обязательно помогут ребенку.
Для чего нужен решебник?
Публикация дает всем учащимся возможность проработать материал самостоятельно, а в случае недопонимания или упущения темы пройти его самостоятельно, не жертвуя качеством. Также справочные данные позволяют эффективно подготовиться к предстоящей самостоятельной и контрольной работе. Самые любознательные ученики могут продвинуться по учебной программе, что в будущем положительно скажется на усвоении знаний и повышении среднего балла.
После 10-11 классов Учебник Алимова по алгебре для 10-11 классов Родители и учителя вполне могут его использовать: для первых он станет инструментом контроля знаний ребенка, а для вторых — основой для разработки своих материалов и тестовых заданий для аудиторных занятий.
Как работает коллекция
Ресурс полностью повторяет структуру учебного пособия. Внутри пользователь имеет возможность просмотреть ответы на 1624 упражнения, а также на задания раздела «Проверьте себя», разбитого на тринадцать глав.Ключи доступны круглосуточно, номер можно найти через поле поиска или через удобную навигацию.
Экспоненциальные уравнения и их системы. Экспоненциальные уравнения. Более сложные случаи. Домашнее задание
Основываясь на этом и применяя теорему о корне, мы находим, что уравнение a x = b имеет один единственный корень, при b> 0 и положительном a не равно единице. Чтобы найти его, вам нужно представить b в виде b = a c.
Тогда очевидно, что с будет решением уравнения a x = a c.
Рассмотрим следующий пример: Решите уравнение 5 (x 2 — 2 * x — 1) = 25.
Представим 25 как 5 2, получим:
5 (x 2 — 2 * x — 1) = 5 2.
Или как эквивалент:
х 2 — 2 * х — 1 = 2.
Решаем получившееся квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.
Ответ: 3; -1.
Решите уравнение 4 x — 5 * 2 x + 4 = 0. Замените t = 2 x и получите следующее квадратное уравнение:
т 2 — 5 * т + 4 = 0.
Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4
Теперь решите уравнения 2 x = 1 и 2 x = 4.
Ответ: 0; 2.
Решение экспоненциальных неравенств
Решение простейших экспоненциальных неравенств также основано на свойствах возрастающих и убывающих функций. Если в экспоненциальной функции основание a больше единицы, то функция будет возрастать во всей области определения.Если в экспоненциальной функции с основанием a выполняется условие 0, то эта функция будет убывающей на всем наборе действительных чисел.
Рассмотрим пример: решим неравенство (0.5) (7 — 3 * x)
Обратите внимание, что 4 = (0,5) 2. Тогда неравенство принимает вид (0,5) (7 — 3 * x)
Получаем: 7 — 3 * x> -2.
Отсюда: x
Ответ: x
Если бы в неравенстве база была больше единицы, то при избавлении от базы знак неравенства менять не нужно.
Урок и презентация на тему: «Экспоненциальные уравнения и экспоненциальные неравенства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное учебное пособие для 9-11 классов «Тригонометрия»
Интерактивное учебное пособие для 10-11 классов «Логарифмы»
Определение экспоненциальных уравнений
Ребята, мы изучали экспоненциальные функции, изучили их свойства и построили графики, проанализировали примеры уравнений, в которых встречались экспоненциальные функции.х = 3 $.На последнем уроке мы узнали, что экспоненциальные выражения могут принимать только положительные значения, запомните график. Следовательно, первое уравнение не имеет решений, второе уравнение имеет одно решение: $ x = 1 $.
Ответ: $ x = 1 $.
Давайте составим контрольный список способов решения экспоненциальных уравнений:
1. Графический метод. Представляем обе части уравнения в виде функций и строим их графики, находим точки пересечения графиков.2-у-12 = 0 $.
$ (y-4) (y + 3) = 0 $.
$ y_1 = 4 $ и $ y_2 = -3 $.
Переходя к исходным переменным, из первого уравнения получаем $ x + y = 2 $. Второе уравнение не имеет решений. Тогда наша исходная система уравнений эквивалентна системе: $ \ begin (cases) x + 3y = 0, \\ x + y = 2. \ end (ases) $.
Вычитая второе из первого уравнения, получаем: $ \ begin (cases) 2y = -2, \\ x + y = 2. \ end (cases) $.
$ \ begin (case) y = -1, \\ x = 3.y = v \ (v> 0) $, получаем:
Рисунок 5.
Решим получившуюся систему методом сложения. Сложим уравнения:
\ \
Тогда из второго уравнения получаем, что
Возвращаясь к замене, я получил новую систему экспоненциальных уравнений:
Рисунок 6.
Получаем:
Рисунок 7.
Ответ: $ (0,1) $.
Системы экспоненциальных неравенств
Определение 2
Системы неравенств, состоящие из экспоненциальных уравнений, называются системой экспоненциальных неравенств.
Рассмотрим решение систем экспоненциальных неравенств на примерах.
Пример 3
Решите систему неравенств
Рисунок 8.
Решение:
Данная система неравенств эквивалентна системе
Рисунок 9.
Для решения первого неравенства вспомним следующую теорему об эквивалентности экспоненциальных неравенств:
Теорема 1.(\ varphi (x)) $, где $ a> 0, a \ ne 1 $ эквивалентно набору двух систем
\}
Как найти объем функции. Диапазон допустимых значений — ODZ. (2019)
Решая различные задачи, нам очень часто приходится проводить идентичные преобразования выражений. Но бывает, что в одних случаях допустима какая-то трансформация, в других — нет. ОДЗ оказывает существенную помощь в части контроля допустимости проводимых преобразований.Остановимся на этом подробнее.
Суть подхода заключается в следующем: ODZ переменных для исходного выражения сравнивается с ODZ переменных для выражения, полученного в результате выполнения идентичных преобразований, и по результатам сравнения делаются соответствующие выводы.
В целом идентичные преобразования могут
- не влияют на LDU;
- приводят к расширению DLU;
- приводят к сужению ОДЗ.
Поясним каждый случай на примере.
Рассмотрим выражение x 2 + x + 3 x, ODZ переменной x для этого выражения — это множество R. форма x 2 + 4 · x. Очевидно, что LDZ переменной x этого выражения также является множеством R. Таким образом, проведенное преобразование не изменило DHS.
Идем дальше. Возьмем выражение x + 3 / x — 3 / x.В этом случае ГРВ определяется условием x ≠ 0, что соответствует набору (−∞, 0) ∪ (0, + ∞). Это выражение также содержит аналогичные члены, после сокращения которых мы приходим к выражению x, для которого ODV равно R. Что мы видим: в результате выполненного преобразования произошло расширение ODZ (число ноль было добавлено к ODZ переменной x для исходного выражения).
Осталось рассмотреть пример сужения диапазона допустимых значений после проведения преобразований.Возьмем выражение … ODL переменной x определяется неравенством (x — 1) · (x — 3) ≥0, для его решения подходит, например, в результате имеем (−∞ , 1] ∪∪; под ред. С.А. Теляковского. — 17-изд. — М .: Просвещение, 2008. — 240 с .: ил. — ISBN 978-5-09-019315-3.
Функция — это модель. Определим X как набор значений независимой переменной // независимое означает любое.
Функция — это правило, по которому для каждого значения независимой переменной из набора X можно найти единственное значение зависимой переменной. // т.е. есть один y для каждого x.
Из определения следует, что существуют два понятия — независимая переменная (которую мы обозначаем x и она может принимать любые значения) и зависимая переменная (которую мы обозначаем y или f (x) и вычисляется из функции когда мы подставляем x).2. (называется параболой)
3.y = 3x + 7. (называется прямой)
4.y = √ x. (называется ветвью параболы)
Независимая переменная (которую мы обозначаем как x) называется аргументом функции.
Объем функций
Набор всех значений, которые принимает аргумент функции, называется областью функции и обозначается D (f) или D (y).
Рассмотрим D (y) для 1., 2., 3., 4.
1. D (y) = (∞; 0) and (0; + ∞) // весь набор действительных чисел, кроме нуля.
2.D (y) = (∞; + ∞) // все много действительных чисел
3.D (y) = (∞; + ∞) // все много действительных чисел
4. D (y) = — ∞; + ∞ [.
Пример 1. Найти область определения функции y = 2 .
Решение. Область определения функции не указывается, что означает, что в силу приведенного выше определения мы имеем в виду естественную область определения. Выражение f ( x ) = 2 определено для любых действительных значений x , следовательно, эта функция определена для всего набора R вещественных числа.
Таким образом, на приведенном выше рисунке числовая линия заштрихована от минус бесконечности до плюс бесконечности.
Корневая область
n -я степеньВ случае, когда функция задана формулой и n — натуральное число:
Пример 2. Найти область определения функции .
Решение. Как следует из определения, четный корень имеет смысл, если радикальное выражение неотрицательно, то есть если — 1 ≤ x ≤ 1.Следовательно, область определения этой функции [- 1; 1].
Заштрихованная область числовой линии на рисунке выше является областью определения этой функции.
Область степенной функции
Область степенной функции с целым показателем
, если a — положительное значение, то область определения функции — это набор всех действительных чисел, то есть] — ∞; + ∞ [;
, если a — отрицательное, то областью определения функции является множество] — ∞; 0 [∪] 0; + ∞ [, то есть вся числовая строка, кроме нуля.
На соответствующем рисунке сверху вся числовая линия заштрихована, а точка, соответствующая нулю, проколота (не входит в область определения функции).
Пример 3. Найти область определения функции .
Решение. Первый член представляет собой целую степень x, равную 3, а степень x во втором члене может быть представлена как единица — также целое число. Следовательно, область определения этой функции — целая числовая прямая, то есть] — ∞; + ∞ [.
Область определения степенной функции с дробным показателем
В случае, если функция задана формулой:
если — положительный, то область определения функции — множество 0; + ∞ [.
Пример 4. Найти область определения функции .
Решение. Оба члена в выражении функции являются степенными функциями с положительными дробными показателями. Следовательно, областью определения этой функции является множество — ∞; + ∞ [.
Область экспоненциальных и логарифмических функций
Область экспоненциальной функции
В случае, когда функция задается формулой, областью определения функции является вся числовая строка, то есть] — ∞; + ∞ [.
Область логарифмической функции
Логарифмическая функция определяется при условии, что ее аргумент положителен, то есть областью ее определения является множество] 0; + ∞ [.
Найдите объем функции самостоятельно, а затем посмотрите решение
Область тригонометрических функций
Объем функции y = cos ( x ) также является набором R вещественных числа.
Объем функции y = tg ( x ) — партии по R вещественных числа, кроме чисел.
Объем функции y = ctg ( x ) — партии по R вещественных числа, кроме чисел.
Пример 8. Найти область определения функции .
Решение. Внешняя функция представляет собой десятичный логарифм, и условия области определения логарифмической функции в целом применяются к области ее определения. То есть ее аргумент должен быть положительным. Аргументом здесь является синус x. Поворачивая воображаемый циркуль по кругу, мы видим, что условие sin x > 0 нарушается, когда «x» равно нулю, «пи», двойке, умноженному на «пи» и обычно равному произведению «пи». «и любое четное или нечетное целое число.
Таким образом, область определения этой функции задается выражением
,
, где k — целое число.
Область обратных тригонометрических функций
Область действия функции y = arcsin ( x ) — набор [-1; 1].
Область действия функции y = arccos ( x ) — также набор [-1; 1].
Объем функции y = arctg ( x ) — партии по R вещественных числа.
Объем функции y = arcctg ( x ) также является набором R вещественных числа.
Пример 9. Найти область определения функции .
Решение. Решим неравенство:
Таким образом, мы получаем область определения этой функции — отрезок [- 4; 4].
Пример 10. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение второго неравенства:
Таким образом, мы получаем область определения этой функции — отрезок.
Область определения дроби
Если функция задается дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является набор R действительных числа, за исключением таких x , у которых знаменатель дроби обращается в нуль.
Пример 11. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби, находим область определения этой функции — множество] — ∞; — 2 [∪] — 2; + ∞ [.
Дробные уравнения. ODZ.
Внимание!
Есть дополнительные
материалов в Спец Разделе 555.
Для тех, кто очень «не очень …»
И для тех, кто «очень …»)
Продолжаем осваивать уравнения. Мы уже умеем работать с линейными и квадратными уравнениями. Остается последний вид — дробных уравнения … Или их еще называют гораздо солиднее — дробно-рациональных уравнений … Это то же самое.
Дробные уравнения.
Как следует из названия, в этих уравнениях всегда присутствуют дроби. Но не просто дроби, а дроби, у которых в знаменателе неизвестно … Хотя бы один. Например:
Напомню, что если в знаменателях всего числа , то это линейные уравнения.
Как решить дробных уравнений ? Прежде всего, избавьтесь от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратичное.И тогда мы знаем, что делать … В некоторых случаях это может превратиться в тождество, например 5 = 5, или неправильное выражение, например 7 = 2. Но такое случается редко. Я упомяну об этом ниже.
Но как избавиться от дробей !? Очень простой. Применяя все те же одинаковые преобразования.
Нам нужно умножить все уравнение на одно и то же выражение. Так что все знаменатели уменьшены! Все сразу станет легче. Позвольте мне объяснить на примере. Допустим, нам нужно решить уравнение:
Как вы учили в младших классах? Переносим все в одну сторону, сводим к общему знаменателю и т. Д.Забыть это как дурной сон! Это нужно делать, когда вы складываете или вычитаете дробные выражения. Или работать с неравенством. И в уравнениях мы сразу же умножаем обе части на выражение, которое даст нам возможность уменьшить все знаменатели (т.е., по сути, на общий знаменатель). А что это за выражение?
Слева, чтобы отменить знаменатель, умножьте на x + 2 … А справа умножьте на 2. Это означает, что уравнение нужно умножить на 2 (x + 2) … Умножаем:
Это обычное умножение дробей, но напишу подробно:
Обратите внимание, что я пока не раскрываю скобки. (х + 2) ! Итак, в целом, я пишу это:
Слева уменьшено полностью (x + 2) , а справа 2. Что и требуется! После приведения получим линейное уравнение:
И это уравнение решит каждый! х = 2 .
Решим еще один пример, посложнее:
Если вспомнить, что 3 = 3/1, а 2x = 2x / 1, можно написать:
И снова избавляемся от того, что нам не очень нравится — дробей.
Мы видим, что для отмены знаменателя с x нужно умножить дробь на (x — 2) … Несколько нам не помеха. Что ж, размножаемся. Вся левая сторона и вся правая сторона:
Опять же скобки (х — 2) не раскрываю.Работаю со скобкой целиком, как с одним числом! Это нужно делать всегда, иначе ничего не уменьшится.
С чувством глубокого удовлетворения разрезаем (x — 2) и получаем уравнение без дробей, в линейке!
А теперь раскроем скобки:
Дарим аналогичные, переносим все в левую часть и получаем:
Но перед этим научимся решать другие задачи.Интерес. Кстати, эти грабли!
Если вам нравится этот сайт …Кстати, у меня для вас есть еще парочка интересных сайтов.)
Вы можете попрактиковаться в решении примеров и узнать свой уровень. Мгновенное проверочное тестирование. Учимся — с интересом!)
Вы можете ознакомиться с функциями и производными.
Объем функции.Примеры. Odz
Любое выражение с переменной имеет свою собственную область допустимых значений, где она существует. При принятии решения всегда необходимо учитывать DLD. При его отсутствии можно получить неверный результат.
Эта статья покажет, как правильно найти ODZ, использовать это на примерах. Также будет учтена важность указания DLD в решении.
Яндекс.РТБ R-A-339285-1
Допустимые и недопустимые значения переменных
Это определение связано с допустимыми значениями переменных.Вводя определение, мы увидим, к какому результату оно приведет.
Начиная с 7 класса мы начинаем работать с числами и числовыми выражениями. Исходные определения с переменными переходят к значениям выражений с выбранными переменными.
Когда есть выражения с выбранными переменными, некоторые из них могут не удовлетворять. Например, выражение вида 1: a, если a = 0, то оно не имеет смысла, так как делить на ноль невозможно. То есть выражение должно иметь такие значения, которые подходят в любом случае и дают ответ.Другими словами, это имеет смысл с доступными переменными.
Определение 1
Если есть выражение с переменными, то оно имеет смысл только тогда, когда при подстановке значение может быть вычислено.
Определение 2
Если есть выражение с переменными, то оно не имеет смысла, когда при подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Определение 3
Существующие допустимые переменные — это те значения, для которых выражение имеет смысл.А если в этом нет смысла, то они считаются недопустимыми.
Чтобы прояснить вышесказанное: если существует более одной переменной, то может быть пара подходящих значений.
Пример 1
В качестве примера рассмотрим выражение вида 1 x — y + z, где есть три переменные. В противном случае можно записать как x = 0, y = 1, z = 2, при этом другая запись имеет вид (0, 1, 2). Эти значения называются действительными, а значит, вы можете найти значение выражения.Получаем, что 1 0 — 1 + 2 = 1 1 = 1. Отсюда видим, что (1, 1, 2) недопустимы. Подстановка приводит к делению на ноль, то есть 1 1-2 + 1 = 1 0.
Что такое DLD?
Диапазон допустимых значений — важный элемент при вычислении алгебраических выражений. Поэтому на это стоит обращать внимание при расчетах.
Определение 4
Область DLD Набор значений, разрешенных для данного выражения.
Рассмотрим пример выражения.
Пример 2
Если у нас есть выражение вида 5 z — 3, то ODZ имеет вид (- ∞, 3) ∪ (3, + ∞). Эта область допустимых значений удовлетворяет переменной z для данного выражения.
Если есть выражения вида z x — y, то можно видеть, что x ≠ y, z принимает любое значение. Это называется выражением ODZ. Это нужно учитывать, чтобы при подстановке не получилось деление на ноль.
Область допустимых значений и область определения имеют то же значение.Только второй из них используется для выражений, а первый — для уравнений или неравенств. Использование DLD имеет смысл, выражение или неравенство. Область определения функции совпадает с областью допустимых значений переменной x до выражения f (x).
Как найти DLD? Примеры, решения
Найти SDL означает найти все допустимые значения, подходящие для данной функции или неравенства. Если эти условия не соблюдены, можно получить неверный результат.Чтобы найти DLD, часто необходимо выполнить преобразования в данном выражении.
Есть выражения, вычисление которых невозможно:
- , если есть деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого числа — только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения касательной π 2 + π · k, k ∈ Z, и котангенса π · k, k ∈ Z;
- нахождение значения арксинуса и арккосинуса числа, значение которого не принадлежит [- 1; один ] .
Все это говорит о том, насколько важно наличие DLD.
Пример 3
Найдите выражения ODZ x 3 + 2 · x · y — 4 .
Решение
В кубе можно возвести любое число. В этом выражении нет дроби, поэтому значения x и y могут быть любыми. То есть ОДЗ — это любое число.
Ответ: x и y — любые значения.
Пример 4
Найдите ODZ выражения 1 3 — x + 1 0.
Решение
Видно, что дробь одна, знаменатель которой равен нулю. Это говорит о том, что для любого значения x мы получим деление на ноль. Итак, можно сделать вывод, что данное выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅.
Пример 5
Найдите ODZ данного выражения x + 2 · y + 3 — 5 · x.
Решение
Наличие квадратного корня предполагает, что это выражение должно быть больше или равно нулю.При отрицательном значении это не имеет смысла. Следовательно, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0. То есть это искомый диапазон допустимых значений.
Ответ: множество x и y, где x + 2 · y + 3 ≥ 0.
Пример 6
Определите выражения ODZ в форме 1 x + 1 — 1 + log x + 8 (x 2 + 3).
Решение
По условию у нас есть дробь, поэтому ее знаменатель не должен быть нулевым.Мы получаем, что x + 1 — 1 ≠ 0. Радикальное выражение всегда имеет смысл, когда оно больше или равно нулю, то есть x + 1 ≥ 0. Поскольку оно имеет логарифм, его выражение должно быть строго положительным, т. Е. x 2 + 3> 0. Основание логарифма также должно иметь положительное значение и отличаться от 1, тогда складываем условия x + 8> 0 и x + 8 ≠ 1. Отсюда следует, что искомая ODZ принимает форма:
x + 1-1 0, x + 1 ≥ 0, x 2 + 3> 0, x + 8> 0, x + 8 ≠ 1
Другими словами, они называют систему неравенств с одной переменной.Решение приведет к такому обозначению ODZ [- 1, 0) ∪ (0, + ∞).
Ответ: [- 1, 0) ∪ (0, + ∞)
Почему важно учитывать DLD при трансформации?
При идентичных трансформациях важно найти ODZ. Бывают случаи, когда существование DLD отсутствует. Чтобы понять, имеет ли решение данное выражение, необходимо сравнить ODZ переменных исходного выражения и ODZ результирующего.
Преобразования личности:
- не может повлиять на DLD;
- может привести к расширению или добавлению DLD;
- может сузить DLD.
Рассмотрим пример.
Пример 7
Если у нас есть выражение вида x 2 + x + 3 · x, то его ODZ определяется для всей области. Даже при сокращении таких членов и упрощении выражения ODL не меняется.
Пример 8
Если мы возьмем пример выражения x + 3 x — 3 x, то все будет по-другому.У нас есть дробное выражение. Но мы знаем, что деление на ноль недопустимо. Тогда ODZ имеет вид (- ∞, 0) ∪ (0, + ∞). Видно, что ноль не является решением, поэтому мы добавляем его в круглые скобки.
Рассмотрим пример с наличием радикального выражения.
Пример 9
Если есть x — 1 · x — 3, то следует обратить внимание на ODZ, так как он должен быть записан в виде неравенства (x — 1) · (x — 3) ≥ 0 Возможно решение интервальным методом, тогда получаем, что ODZ принимает вид (- ∞, 1] ∪ [3, + ∞).После преобразования x — 1 · x — 3 и применения свойства корней получаем, что ODZ можно дополнить и записать в виде системы неравенств вида x — 1 ≥ 0, x — 3 ≥ 0. Решая ее, мы получим [3, + ∞). Следовательно, DLD полностью записывается следующим образом: (- ∞, 1] ∪ [3, + ∞).
Следует избегать преобразований, сужающих DLD.
Пример 10
Рассмотрим на примере выражения x — 1 · x — 3 при x = — 1. При подстановке получаем, что — 1 — 1 · — 1 — 3 = 8 = 2 2.Если преобразовать это выражение и привести его к виду x — 1 · x — 3, то при вычислении получим, что 2 — 1 · 2 — 3 выражение не имеет смысла, так как радикальное выражение не должно быть отрицательным.
Надо придерживаться идентичных преобразований, что ODZ менять не будет.
Если есть примеры, расширяющие его, то его нужно добавить в DLD.
Пример 11
Рассмотрим дробь в форме x x 3 + x в качестве примера. Если мы сократим на x, то получим 1 x 2 + 1.Затем DLD расширяется и становится (- ∞ 0) ∪ (0, + ∞). Причем при вычислении мы уже работаем со второй упрощенной дробью.
С логарифмами дело обстоит немного иначе.
Пример 12
Если существует выражение вида ln x + ln (x + 3), оно заменяется на ln (x · (x + 3)) на основании свойства логарифма. Это показывает, что DLD от (0, + ∞) до (- ∞, — 3) ∪ (0, + ∞). Следовательно, чтобы определить DLD ln (x · (x + 3)), необходимо произвести вычисления на DLD, то есть (0, + ∞) множествах.
При принятии решения всегда необходимо обращать внимание на структуру и внешний вид условно заданного выражения. Если домен определения найден правильно, результат будет положительным.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и дайте нам знать, если у вас возникнут какие-либо вопросы.
Сбор и использование личной информации
Личная информация — это данные, которые могут быть использованы для идентификации конкретного человека или для связи с ним.
Вас могут попросить предоставить вашу личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете запрос на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. Д.
Как мы используем вашу личную информацию:
- Собираемая нами личная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях, а также предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, например, для проведения аудита, анализа данных и различных исследований, чтобы улучшить предоставляемые нами услуги и дать вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- При необходимости — в соответствии с законом, судебной системой, в ходе судебного разбирательства и / или на основании публичных запросов или запросов государственных органов в Российской Федерации — раскрывайте вашу личную информацию.Мы также можем раскрыть информацию о вас, если мы определим, что такое раскрытие необходимо или целесообразно в целях безопасности, поддержания правопорядка или в других социально значимых случаях.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующей третьей стороне, правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности — включая административные, технические и физические — для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Обеспечение конфиденциальности на уровне вашей компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам правила конфиденциальности и безопасности и строго следим за соблюдением мер конфиденциальности.
Решая различные задачи, нам очень часто приходится проводить идентичные преобразования выражений. Но бывает, что в одних случаях допустима какая-то трансформация, в других — нет. Значительную помощь с точки зрения мониторинга допустимости проводимых реформ оказывает ОДЗ.Остановимся на этом подробнее.
Суть подхода заключается в следующем: сравнивая переменные ODZ для исходного выражения с переменными ODZ для выражения, полученного в результате выполнения идентичных преобразований, и по результатам сравнения делаются соответствующие выводы.
Как правило, преобразования идентичности могут
- не влияет на DLD;
- приведет к расширению междугородной телефонной сети;
- приведет к сужению DLD.
Поясним каждый случай на примере.
Рассмотрим выражение x 2 + x + 3 · x, ODZ переменной x для этого выражения — это множество R. Теперь давайте проделаем следующее идентичное преобразование с этим выражением — мы представим аналогичные термины, в результате форма x 2 + 4 · x. Очевидно, что переменная x DLD этого выражения также является множеством R. Таким образом, преобразование не изменило DLD.
Идем дальше. Возьмем выражение x + 3 / x — 3 / x.В этом случае DLD определяется условием x ≠ 0, что соответствует набору (−∞, 0) ∪ (0, + ∞). Это выражение также содержит аналогичные слагаемые, после сокращения которых мы приходим к выражению x, для которого ODZ равно R. Что мы видим: в результате преобразования произошло расширение ODZ (число ноль было добавлено к ODZ переменной x для исходного выражения).
Осталось рассмотреть пример сужения диапазона допустимых значений после преобразований.Возьмите выражение. DLD переменной x определяется неравенством (x — 1) · (x — 3) ≥0, оно подходит для своего решения, например, в результате имеем (−∞, 1] ∪∪; отредактировано С.А. Теляковского. — 17-е изд. — М .: Просвещение, 2008. — 240 с .: ил. — ISBN 978-5-09-019315-3.
Как найти объем функции? Ученикам средней школы часто приходится сталкиваться с этой задачей.
Родители должны помочь своим детям разобраться в этом.
Должностная функция.
Напомним основные термины алгебры. Функция в математике — это зависимость одной переменной от другой. Можно сказать, что это строгий математический закон, который определенным образом связывает два числа.
В математике при анализе формул числовые переменные заменяются буквенными символами. Чаще всего используются x («x») и gamer («y»). Переменная x называется аргументом, а переменная y называется зависимой переменной или функцией от x.
Существуют различные способы определения зависимостей переменных.
Перечислим их:
- Аналитический тип.
- Табличный вид.
- Графический дисплей.
Аналитический метод представлен формулой.Рассмотрим примеры: y = 2x + 3, y = log (x), y = sin (x). Формула y = 2x + 3 типична для линейной функции. Подставляя числовое значение аргумента в данную формулу, получаем значение y.
Табличный метод представляет собой таблицу, состоящую из двух столбцов. Первый столбец предназначен для значений x, а следующий столбец записывает данные игры.
Графический метод считается наиболее интуитивно понятным. Граф — это отображение множества всех точек на плоскости.
Для построения диаграммы используется декартова система координат. Система состоит из двух перпендикулярных линий. На оси укладывают одинаковые сегменты агрегата. Отсчет времени ведется от центральной точки пересечения прямых.
Независимая переменная отображается на горизонтальной линии. Она называется осью абсцисс. Вертикальная линия (ось ординат) отображает числовое значение зависимой переменной. На пересечении перпендикуляров к этим осям отмечаются точки.Соединяя точки вместе, получаем сплошную линию. Это основа расписания.
Типы переменных зависимостей
Определение
В целом зависимость представляется в виде уравнения: y = f (x). Из формулы следует, что для каждого значения числа x существует определенное число y. Значение игры, соответствующее числу x, называется значением функции.
Все возможные значения, требуемые независимой переменной, образуют область определения функции.Соответственно, весь набор чисел зависимой переменной определяет диапазон значений функции. Область видимости — это все значения аргументов, для которых имеет смысл f (x).
Первоначальная задача при изучении математических законов — найти область определения. Этот термин следует правильно определить. В противном случае все дальнейшие расчеты будут бесполезны. Ведь объем ценностей формируется на основе элементов первого набора.
Объем функции напрямую зависит от ограничений.Ограничения связаны с невозможностью выполнять определенные операции. Есть также ограничения на применение числовых значений.
При отсутствии ограничений областью определения является все числовое пространство. Знак бесконечности имеет горизонтальную восьмерку. Весь набор чисел записывается так: (-∞; ∞).
В некоторых случаях массив данных состоит из нескольких подмножеств. Объем числовых пропусков или пробелов зависит от типа закона изменения параметров.
Перечислим факторы, влияющие на ограничения:
- обратная пропорциональность;
- корень арифметический;
- возведение в степень;
- логарифмическая зависимость;
- тригонометрических форм.
Если таких элементов несколько, то поиск ограничений для каждого из них прекращается. Самая большая проблема — это выявление критических точек и пробелов. Решением проблемы будет объединение всех числовых подмножеств.
Набор и подмножество чисел
О наборах.
Область обозначена как D (f), а знак объединения представлен символом ∪. Все числовые пробелы заключены в квадратные скобки. Если граница участка не входит в набор, то поставить полукруглую скобу. В противном случае, когда число включено в подмножество, используются квадратные скобки.
Обратная пропорциональность выражается формулой y = k / x. График функции представляет собой изогнутую линию, состоящую из двух ветвей.Это обычно называют гиперболой.
Поскольку функция выражается в виде дроби, поиск области определения сводится к анализу знаменателя. Хорошо известно, что деление на ноль запрещено в математике. Решение проблемы — приравнять знаменатель к нулю и найти корни.
Вот пример:
Устанавливается: y = 1 / (x + 4). Найдите прицел.
- Обнулить знаменатель.
х + 4 = 0 - Найдите корень уравнения.
х = -4 - Определяем набор всех возможных значений аргумента.
D (f) = (- ∞; -4) ∪ (-4; + ∞)
Ответ: объем функции — все действительные числа, кроме -4.
Значение числа под знаком квадратного корня не может быть отрицательным. В этом случае определение функции сводится к решению неравенства. Корневое выражение должно быть больше нуля.
Область определения корня связана с четностью корневого индекса.Если показатель делится на 2, то выражение имеет смысл только в том случае, если оно положительное. Нечетный номер индикатора указывает на правильность любого значения радикального выражения: как положительного, так и отрицательного.
Неравенство решается так же, как и уравнение. Есть только одно отличие. После умножения обеих частей неравенства на отрицательное число знак следует поменять местами.
Если в знаменателе стоит квадратный корень, необходимо наложить дополнительное условие.Значение числа не должно быть нулевым. Неравенство переходит в разряд строгих неравенств.
Логарифмические и тригонометрические функции
Логарифмическая форма имеет смысл для положительных чисел. Таким образом, область определения логарифмической функции аналогична функции извлечения квадратного корня, за исключением нуля.
Рассмотрим пример логарифмической зависимости: y = log (2x-6). Найдите прицел.
- 2х-6> 0
- 2x> 6
- х> 6/2
Ответ: (3; + ∞).
Область значений y = sin x и y = cos x — это набор всех действительных чисел. Есть ограничения на тангенс и котангенс. Они связаны с делением угла на косинус или синус.
Тангенс угла определяется отношением синуса к косинусу. Указываем значения углов, при которых значение тангенса не существует. Функция y = tg x имеет смысл для всех значений аргумента, кроме x = π / 2 + πn, n∈Z.
Область определения функции y = ctg x — это весь набор действительных чисел, исключая x = πn, n∈Z. Если аргумент равен числу π или кратно π, синус угла равен нулю. В этих точках (асимптотах) котангенс существовать не может.
Первые задания по определению предметной области начинаются на уроках 7 класса. При первом знакомстве с этим разделом алгебры ученик должен четко понимать тему.
Следует отметить, что этот семестр будет сопровождать студента, а затем и студента на протяжении всего периода обучения.
Функция — это модель. Определяем X как набор значений независимой переменной // независимое означает любое.
Функция — это правило, по которому для каждого значения независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого x есть один y.
Из определения следует, что есть два понятия: независимая переменная (которую мы обозначаем x, и она может принимать любые значения) и зависимая переменная (которую мы обозначаем y или f (x), и она вычисляется из функции, когда мы заменить x).2. (называется параболой)
3.y = 3x + 7. (называется прямым)
4.y = √ x. (называется ветвью параболы)
Независимая переменная (которую мы обозначаем x) называется аргументом функции.
Область определения функции
Набор всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (y) для 1., 2., 3., 4.
1. D (y) = (∞; 0) and (0; + ∞) // весь набор действительных чисел, кроме нуля.
2. D (y) = (∞; + ∞) // все множество действительных чисел
3.



 А.Алимов, Ю.М.Колягин, М.В.Ткачёва и др.)
А.Алимов, Ю.М.Колягин, М.В.Ткачёва и др.) 09
09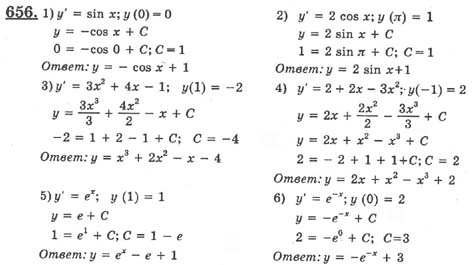 09
09 09
09