Контрольная работа № 1. Векторы в пространстве | |
1 вариант.
А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ). Найдите координаты вектора , если ВМ – медиана ∆АВС. | 2 вариант.
А(6; 3; -2), В(2; 4; -5).
А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ). Найдите координаты вектора , если АМ – медиана ∆АВС. |
Контрольная работа № 2 . Метод координат в пространстве | |
1 вариант
Найти: а) ; б) значение т, при котором .
если А(3; -1; 3), В(3; -2; 2), С(2; 2; 3) и D(1; 2; 2).
| 2 вариант 1. Даны векторы , и , причем: Найти: а) ; б) значение т, при котором .
если А(1; 1; 2), В(0; 1; 1), С(2; -2; 2) и D(2; -3; 1).
|
Контрольная работа № 3. Цилиндр. Конус и шар | |
1 вариант 1. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее. 2. Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см. 3. Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения. | 2 вариант 1. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра. 2. Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см. 3. Образующая конуса l наклонена к плоскости основания под углом в 300. Найдите высоту конуса и площадь осевого сечения. |
Контрольная работа № 4 Объемы тел. Объем призмы, цилиндра, конуса | |
1 вариант 1. Образующая конуса равна 60 см, высота 30 см. Найдите объём конуса. 2. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом 450. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы. 3. Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите объем цилиндра. | 2 вариант 1. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 300. Найдите объём конуса. 2. Основанием прямой призмы является ромб со стороной 12 см и углом 600. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы. 3. Осевым сечением цилиндра является квадрат, диагональ которого равна см. |
Контрольная работа № 5. Объем шара и площадь сферы | |
1 вариант 1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 600. Найдите отношение объёмов конуса и шара. 2. Объём цилиндра равен 96π см3, площадь его осевого сечения 48см2. Найдите площадь сферы, описанной около цилиндра. 3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол . Найдите объём конуса. | 2 вариант 1. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра. 2. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса. 3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол . Найдите объём цилиндра. |
Геометрия 10. Контрольные работы. Атанасян Л.С. | Учебно-методический материал по геометрии (10 класс):
Контрольная работа по геометрии
«Планиметрия»
1 вариант
- Докажите, что если трапеция вписана в окружность, то она равнобедренная.
- На окружности радиуса R последовательно отмечены точки A, B,C, D так, что величины дуг АВ и ВС равны 50˚ и 80˚, диагонали четырехугольника ABCD равны между собой. Найти длину наибольшей стороны четырехугольника.
- Отрезок СН – высота прямоугольного треугольника АВС (). HL =3HK, где HL и HK – биссектрисы треугольников ВСН и АСН соответственно, АВ = . Найти площадь треугольника АВС.
Контрольная работа по геометрии
«Планиметрия»
2 вариант
- Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВC и АD в точках N и Н соответственно.
 Докажите, что BN = DН.
Докажите, что BN = DН. - На окружности радиуса R последовательно отмечены точки K, M, N, Q так, что величины дуг КМ и MN равны 40˚ и 100˚, хорды KN и MQ пересекаются под углом 70˚. Найти длину наибольшей стороны четырехугольника.
- В прямоугольном треугольнике АВС () проведена высота СН. Отрезки АМ и СР – медианы треугольников АСН и НСВ, причем 3АМ = 4СР. Найти радиус окружности, описанной около треугольника АВС, если его площадь равна 96.
……………………………………………………………………………………………………
Контрольная работа по геометрии №1
«Взаимное расположение прямых в пространстве»
1 вариант
- Прямая а параллельна плоскости , прямая в лежит в плоскости . Определите, могут ли прямые а и в:
а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.
- Прямая МА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.
а) Докажите, что МА и ВС – скрещивающиеся прямые.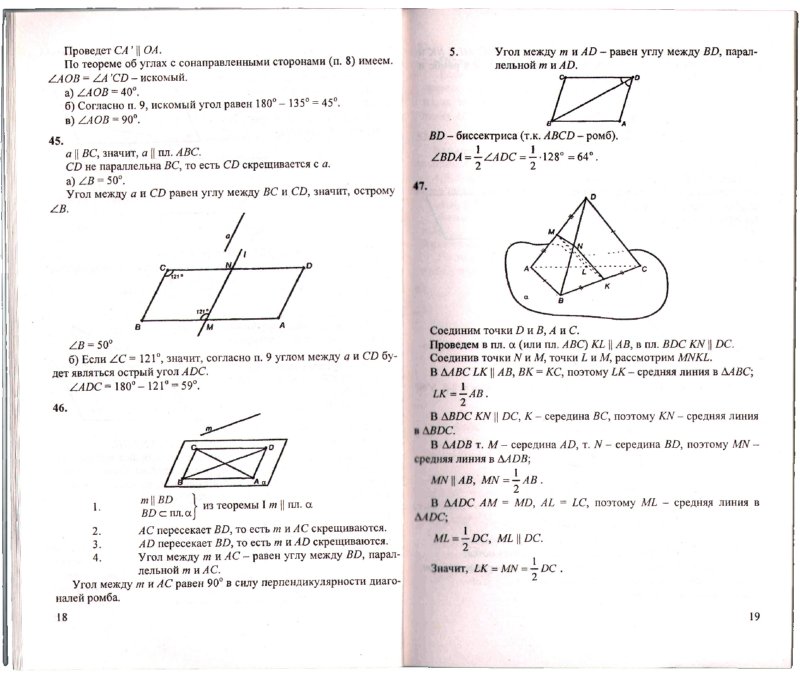
б) Найдите угол между прямыми МА и ВС, если ∠МАD = 45˚.
- Плоскость проходит через середины боковых сторон АВ и СD трапеции ABCD – точки M и N.
а) Докажите, что AD║.
б) Найдите ВС, если AD = 10 см, MN = 8 см.
- (Дополнительно) Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник – ромб.
Контрольная работа по геометрии №1
«Взаимное расположение прямых в пространстве»
2 вариант
- Прямая а параллельна плоскости , прямая в пересекает плоскость . Определите, могут ли прямые а и в:
а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.
 Е и F – середины отрезков АВ и ВС
Е и F – середины отрезков АВ и ВС
а) Докажите, что СD и EF – скрещивающиеся прямые.
б) Найдите угол между прямыми СD и EF, если ∠DСА= 60˚.
- Плоскость проходит через основание АD трапеции ABCD. M и N – середины боковых сторон трапеции
а) Докажите, что MN║.
б) Найдите AD, если ВС = 4 см, MN = 6 см.
- (Дополнительно) Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник – ромб.
…………………………………………………………………………………………………………..
Контрольная работа по геометрии №1.2 Г — 10
«Параллельность плоскостей»
1 вариант
- В тетраэдре ABCD точки М, К и Р – соответственно середины ребер АВ, BD и ВС.
 Доказать, что плоскость МКР параллельна плоскости ACD и найти площадь ΔМКР, если площадь Δ ACD равна 48 см2.
Доказать, что плоскость МКР параллельна плоскости ACD и найти площадь ΔМКР, если площадь Δ ACD равна 48 см2. - Дан параллелепипед ABCDA1B1C1D1. Построить сечение параллелепипеда плоскостью, проходящей через середину ребра AD, параллельно плоскости АСС1.
- Прямые а и в лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными, б) скрещивающимися?
Сделать рисунок для каждого случая. Объяснить.
Контрольная работа по геометрии №1.2 Г — 10
«Параллельность плоскостей»
2 вариант
- В тетраэдре ABCD точки М, К и Р – соответственно середины ребер АD, BD и DС. Доказать, что плоскость МКР параллельна плоскости AВC и найти площадь ΔАВС, если площадь Δ МКР равна 48 см2.
- Дан параллелепипед ABCDA1B1C1D1. Построить сечение параллелепипеда плоскостью, проходящей через середину ребра AВ, параллельно плоскости DBB1.
- Прямые а и в лежат в пересекающихся плоскостях α и β.
 Могут ли эти прямые быть: а) параллельными, б) скрещивающимися?
Могут ли эти прямые быть: а) параллельными, б) скрещивающимися?
Сделать рисунок для каждого случая. Объяснить.
——————————————————————————————————————
Контрольная работа № 2.1 Г — 10
«Перпендикулярность прямых и плоскостей»
1 вариант
- В прямоугольном параллелепипеде ABCDA1B1C1D1 DB1 = 21 см, CD = 16 см, В1С1 = 11 см. Найти длину ребра ВВ1 и синус угла между диагональю DB1 и плоскостью ABCD.
- Длина стороны ромба ABCD равна 5 см, длина диагонали BD равна 6см. Через точку О пересечения диагоналей ромба проведена прямая ОК, перпендикулярная его плоскости. Найти расстояние от точки К до вершин ромба, если ОК = 8см.
- Длина катета прямоугольного равнобедренного треугольника равна 4 см. Плоскость α, проходящая через катет, образует с плоскостью треугольника угол, величина которого равна 30°.
 Найти длину проекции гипотенузы на плоскость α.
Найти длину проекции гипотенузы на плоскость α.
Контрольная работа № 2.1 Г — 10
«Перпендикулярность прямых и плоскостей»
2 вариант
- В прямоугольном параллелепипеде ABCDA1B1C1D1: СА1 = 11 см, C1D1 = 2 см, А1D1 = 6 см. Найти длину ребра СС1 и синус угла между диагональю СА1 и плоскостью ABCD.
- Длины сторон прямоугольника равны 8см и 6см. Через точку О пересечения его диагоналей проведена прямая ОК, перпендикулярная его плоскости. Найти расстояние от точки К до вершин прямоугольника, если ОК = 12 см.
- В треугольнике АВС: ВС = 15 см, АВ = 13 см, АС = 4 см. Через сторону АС проведена плоскость α, составляющая с плоскостью данного треугольника угол 30°. Найти расстояние от вершины В до плоскости α.
………………………………………………………………………………………………….
Контрольная работа №3.1 (1уровень сложности)
«Многогранники»
1 вариант
- Основание прямой призмы – прямоугольный треугольник с катетами 6 см и 8 см.
 Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань – квадрат.
Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань – квадрат.
- Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45 º.
а) Найдите высоту пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
- Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.
Контрольная работа №3.1 (1уровень сложности)
«Многогранники»
2 вариант
- Основание прямой призмы – прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань – квадрат.
- Высота правильной четырехугольной пирамиды равна см, а боковое ребро наклонено к плоскости основания под углом 60º.
а) Найдите боковое ребро пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
- Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середины ребер DA и АВ параллельно ребру ВС, и найдите площадь этого сечения.
……………………………………………………………………………………………………
Контрольная работа №3.1 (2уровень сложности)
«Многогранники»
1 вариант
- Основание прямого параллелепипеда – ромб с диагоналями 10 см и 24 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45º. Найдите площадь полной поверхности параллелепипеда.
- Основание пирамиды – правильный треугольник с площадью см2. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья – наклонена к ней под углом 30º.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
- Ребро куба АВСDA1B1C1D1 равно а. Постройте сечение куба, проходящее через прямую В1С и середину ребра АD, и найдите площадь этого сечения.

Контрольная работа №3.1 (2уровень сложности)
«Многогранники»
2 вариант
- Основание прямого параллелепипеда – ромб с меньшей диагональю 12 см. Большая диагональ параллелепипеда равна см и образует с боковым ребром угол 45º. Найдите площадь полной поверхности параллелепипеда.
- Основание пирамиды – равнобедренный прямоугольный треугольник с гипотенузой см. Боковые грани, содержащие катеты треугольника, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом 45º.
а) Найдите длины боковых ребер пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
- Ребро куба АВСDA1B1C1D1 равно а. Постройте сечение куба, проходящее через точку С и середину ребра AD параллельно прямой DA1, и найдите площадь этого сечения.
……………………………………………………………………………………………………
Контрольная работа по геометрии №3
«Призма. Пирамида»
1 вариант
- Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм АВСD со сторонами 6 дм и 12 дм и углом, равным 60˚.
 Диагональ В1D призмы образует с плоскостью основания угол в 30˚. Найти площадь боковой поверхности призмы.
Диагональ В1D призмы образует с плоскостью основания угол в 30˚. Найти площадь боковой поверхности призмы. - Сторона основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45˚. Найти площадь полной поверхности пирамиды.
Контрольная работа по геометрии №3
«Призма. Пирамида»
2 вариант
- Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм АВСD со сторонами 4 см и см и углом, равным 30˚. Диагональ АС1 призмы образует с плоскостью основания угол в 60˚. Найти площадь боковой поверхности призмы.
- Высота основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45˚. Найти площадь полной поверхности пирамиды.
…………………………………………………………………………………………………
Контрольная работа по геометрии № 4.
«Перпендикулярность прямых и плоскостей».
I вариант
1) Через вершину К треугольника МКР проведена прямая KN, перпендикулярная к плоскости треугольника.


 Найдите расстояние от этой точки до координатных плоскостей.
Найдите расстояние от этой точки до координатных плоскостей.

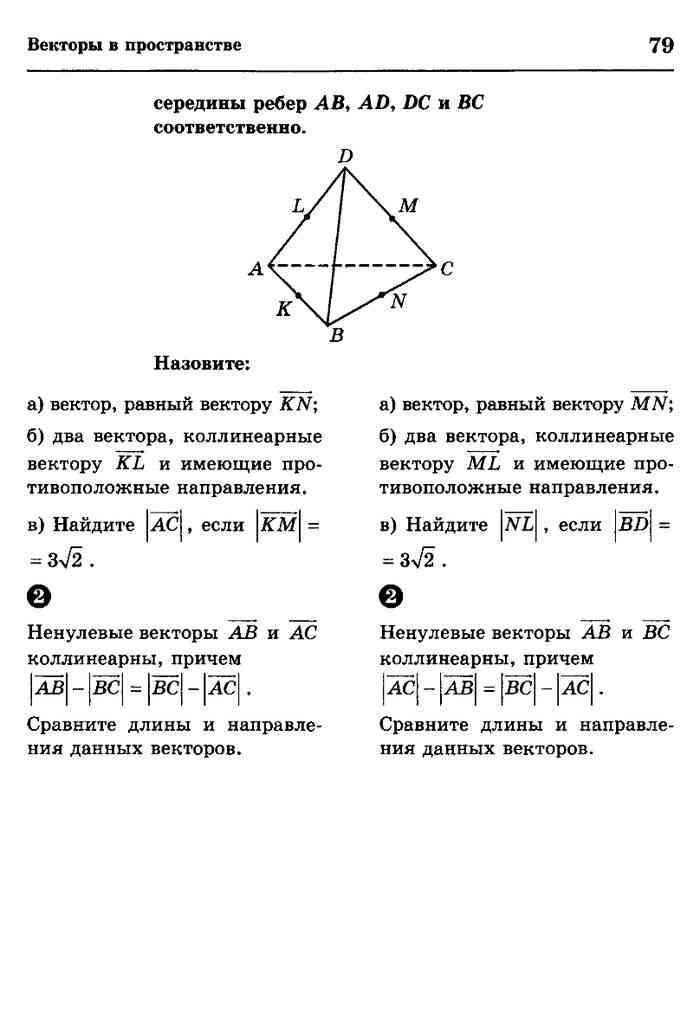 Найдите объем цилиндра.
Найдите объем цилиндра.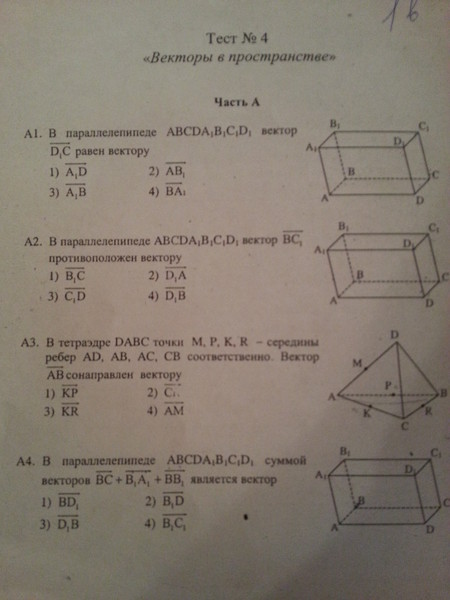
 Докажите, что BN = DН.
Докажите, что BN = DН. Е и F – середины отрезков АВ и ВС
Е и F – середины отрезков АВ и ВС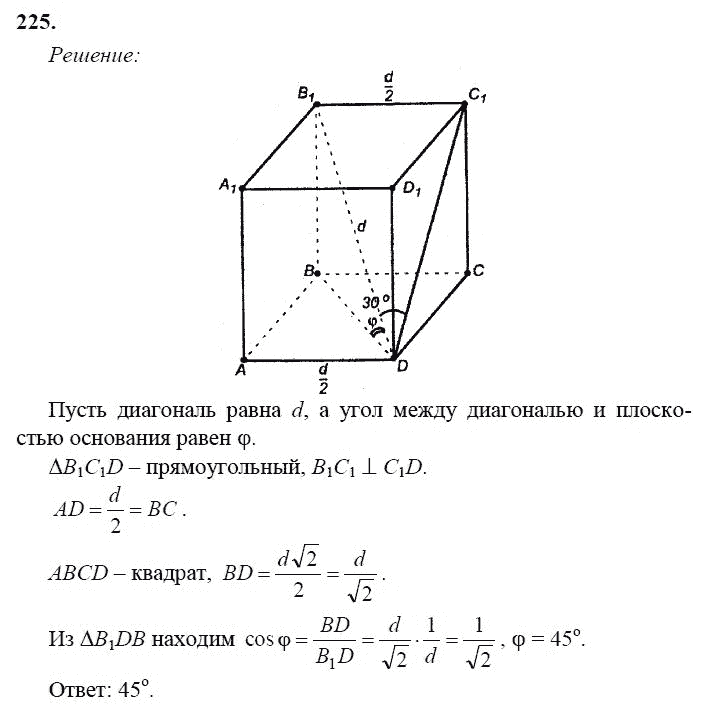 Доказать, что плоскость МКР параллельна плоскости ACD и найти площадь ΔМКР, если площадь Δ ACD равна 48 см2.
Доказать, что плоскость МКР параллельна плоскости ACD и найти площадь ΔМКР, если площадь Δ ACD равна 48 см2. Могут ли эти прямые быть: а) параллельными, б) скрещивающимися?
Могут ли эти прямые быть: а) параллельными, б) скрещивающимися? Найти длину проекции гипотенузы на плоскость α.
Найти длину проекции гипотенузы на плоскость α.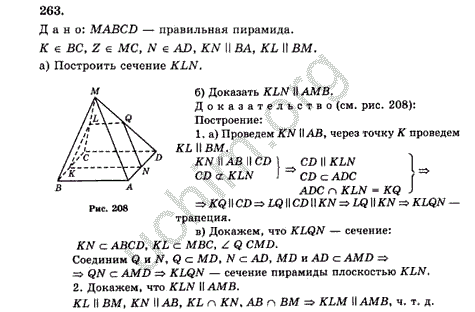 Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань – квадрат.
Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань – квадрат.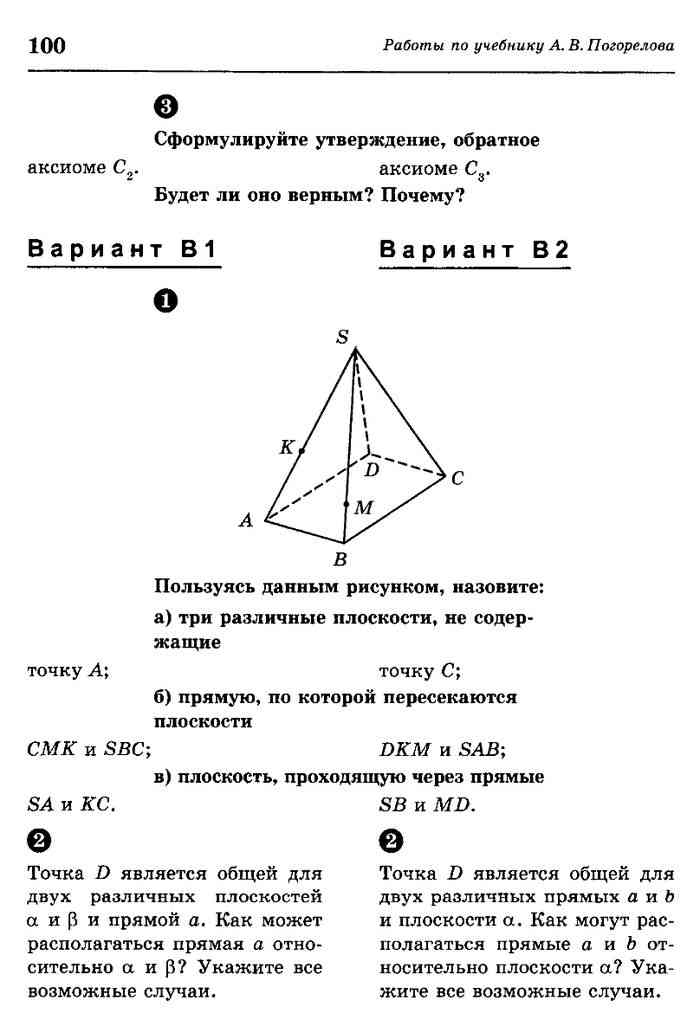
 Диагональ В1D призмы образует с плоскостью основания угол в 30˚. Найти площадь боковой поверхности призмы.
Диагональ В1D призмы образует с плоскостью основания угол в 30˚. Найти площадь боковой поверхности призмы.