Ответы 10 класс геометрия ершова: ГДЗ по Геометрии за 10 класс Самостоятельные и контрольные работы Ершова А.П., Голобородько В.В.

ГДЗ по геометрии для 10 класса самостоятельные и контрольные работы Ершова А.П.

К учебнику Атанасяна. Решения

Самостоятельные работы

СА-1

А1 А2 Б1 Б2 В1 В2

СА-2

А1 А2 Б1 Б2 В1 В2

СА-3

А1 А2 Б1 Б2 В1 В2

СА-4

А1 А2 Б1 Б2 В1 В2

СА-5

А1 А2 Б1 Б2 В1 В2

СА-6

А1 А2 Б1 Б2 В1 В2

СА-7

Вариант 1 Вариант 2

СА-8

А1 А2 Б1 Б2 В1 В2

СА-9

А1 А2 Б1 Б2 В1 В2

СА-10

А1 А2 Б1 Б2 В1 В2

СА-11

Вариант 1 Вариант 2

СА-12

А1 А2 Б1 Б2 В1 В2

СА-13

А1 А2 Б1 Б2 В1 В2

СА-14

А1 А2 Б1 Б2 В1 В2

СА-15

А1 А2 Б1 Б2 В1 В2

СА-16

А1 А2 Б1 Б2 В1 В2

СА-17

А1 А2 Б1 Б2 В1 В2

СА-18

Вариант 1 Вариант 2

СА-19

А1 А2 Б1 Б2 В1 В2

СА-20

А1 А2 Б1 Б2 В1 В2

СА-21

А1 А2 Б1 Б2 В1 В2

СА-22

А1 А2 Б1 Б2 В1 В2

СА-23

А1 А2 Б1 Б2 В1 В2

СА-24

А1 А2 Б1 Б2 В1 В2

СА-25

Вариант 1 Вариант 2

СА-26

А1 А2 Б1 Б2 В1 В2

СА-27

А1 А2 Б1 Б2 В1 В2

СА-28

А1 А2 Б1 Б2 В1 В2

СА-29

Вариант 1 Вариант 2

Контрольные работы

КА-1

А1 А2 Б1 Б2 В1 В2

КА-2

А1 А2 Б1 Б2 В1 В2

КА-3

А1 А2 Б1 Б2 В1 В2

КА-4

А1 А2 Б1 Б2 В1 В2

КА-5

А1 А2 Б1 Б2 В1 В2

Решения»> К учебнику Погорелова. Решения

Самостоятельные работы

СП-1

А1 А2 Б1 Б2 В1 В2

СП-2

А1 А2 Б1 Б2 В1 В2

СП-3

А1 А2 Б1 Б2 В1 В2

СП-4

А1 А2 Б1 Б2 В1 В2

СП-5

А1 А2 Б1 Б2 В1 В2

СП-6

А1 А2 Б1 Б2 В1 В2

СП-7

Вариант 1 Вариант 2

СП-8

А1 А2 Б1 Б2 В1 В2

СП-9

А1 А2 Б1 Б2 В1 В2

СП-10

А1 А2 Б1 Б2 В1 В2

СП-11

А1 А2 Б1 Б2 В1 В2

СП-12

А1 А2 Б1 Б2 В1 В2

СП-13

А1 А2 Б1 Б2 В1 В2

СП-14

Вариант 1 Вариант 2

СП-15

А1 А2 Б1 Б2 В1 В2

СП-16

А1 А2 Б1 Б2 В1 В2

СП-17

А1 А2 Б1 Б2 В1 В2

СП-18

А1 А2 Б1 Б2 В1 В2

СП-19

А1 А2 Б1 Б2 В1 В2

СП-20

А1 А2 Б1 Б2 В1 В2

СП-21

Вариант 1 Вариант 2

СП-22

Вариант 1 Вариант 2

Контрольные работы

КП-1

А1 А2 Б1 Б2 В1 В2

КП-2

А1 А2 Б1 Б2 В1 В2

КП-3

А1 А2 Б1 Б2 В1 В2

КП-4

А1 А2 Б1 Б2 В1 В2

КП-5

А1 А2 Б1 Б2 В1 В2

КП-6

А1 А2 Б1 Б2 В1 В2

вопросы и ответы – Рамблер/класс

6686 вопросов

6752 ответа

1. В равнобедренном треугольнике с периметром 35 см боковая сторона в 2 раза больше основания. А.П. Ершова Геометрия 7 класс. КП-3 Вариант А 2

1.
В равнобедренном треугольнике с периметром 35 см боковая сторона в 2 раза больше основания. Найдите стороны треугольника. (Подробнее…)

ГДЗЕршова А.П.7 классГеометрия

2. Постройте равнобедренный треугольник по боковой стороне и высоте, проведенной из вершины… Геометрия 7 класс А.П. Ершова. СП-13 Вариант В-2

2.
Постройте равнобедренный
треугольник  (Подробнее…)

ГДЗГеометрия7 классЕршова А.П.

В прямом параллелепипеде ABCDA1B1C1D1 AD = 17, DC = 28, АС = 39. Диагональ… 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 14. Вариант 6

В прямом параллелепипеде ABCDA1B1C1D1 AD = 17, DC = 28, АС = 39. Диагональ боковой грани A1D составляет с плоскостью боковой грани (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

В пирамиде DABC AD=4√3 см и перпендикулярно основанию.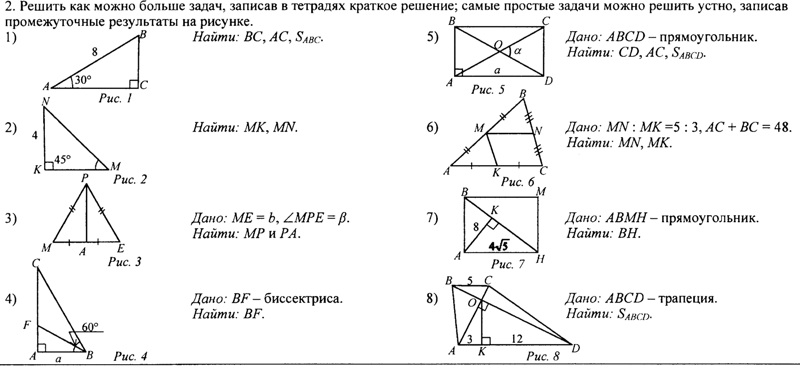 .. 10 класс Геометрия Зив Б.Г. Самостоятельная работа 23. Вариант 4

(Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

1. Найдите расстояние от точки М до прямой CD. Геометрия 10 класс Зив Б.Г. Самостоятельная работа 10. Вариант 3

(Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

ГДЗ по геометрии Атанасян 8 класс. Гл.VIII №787. Выразите вектор…

Необходимо решить задание Гл.VIII №787, нужна помощь.
Точка О — середина медианы EG треугольника DEF. Выразите вектор
(Подробнее…)

ГДЗ8 классАтанасян Л.С.Геометрия

1. На отрезке АВ выбраны точки М и N. Известно, что АВ — 12 см, АМ = 8 см, ВN = = 10 см. 7 класс А.П. Ершова Геометрия. СП-1 Вариант Б 1.

1.
На отрезке АВ выбраны точки М и N. Известно, что
АВ — 12 см, АМ = 8 см, ВN = (Подробнее…)

ГДЗЕршова А.П.Геометрия7 класс

2. В прямоугольном треугольнике АВС гипотенуза АС равна 16 см. Высота ВБ делит угол В… 7 класс А.П. Ершова Геометрия. СП-10 Вариант 2

2.
В прямоугольном треугольнике АВС гипотенуза АС равна
16 см. Высота ВБ делит угол (Подробнее…)

ГДЗЕршова А.П.7 классГеометрия

1. Дан параллелепипед ABCDA1B Представьте вектор АА1 как алгебраическую… 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 20. Вариант 7

1.    Дан параллелепипед ABCDA1B Представьте вектор АА1 как алгебраическую сумму векторов DC1 и DB1.

ГДЗГеометрияЗив Б. Г.10 класс

1. Сторона основания правильной четырехугольной призмы равна 4 см… Геометрия 10 класс Зив Б.Г. Математический диктант 3. Вариант 1

1.        Сторона основания правильной четырехугольной призмы ABCDA1B1C1D1 равна 4 см, а боковое ребро равно 5 см. Найдите площадь (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

3. Изобразите равнобедренный треугольник АВС, у которого. .. 10 класс Геометрия Зив Б.Г. Доп. Самостоятельные работы 1. Вариант 4

3.
Изобразите равнобедренный треугольник АВС, у которого АВ = ВС = 4 и АС = 5, с центром вписанной в треугольник окружности. (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

2. На рисунке 23 точки Е, F, Р и М — середины отрезков AD, CD, ВС и АВ… Геометрия Зив Б.Г. 10 класс. Самостоятельная работа 2. Вариант 5

2. На рисунке 23 точки Е, F, Р и М — середины отрезков AD, CD, ВС и АВ соответственно. Докажите, что ЕР и MF пересекаются и точкой (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

2. Прямые АВ и CD параллельны. Через эти прямые проведены соответственно… Зив Б.Г. 10 класс Геометрия. Самостоятельная работа 19. Вариант 3

(Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

2. Концы отрезков АВ и CD лежат на параллельных плоскостях α и β. Постройте… Зив Б.Г. 10 класс Геометрия. Самостоятельная работа 4. Вариант 2

2. Концы отрезков АВ и CD лежат на параллельных плоскостях α и β (рис. 8). Постройте линии пересечения плоскости АВС с плоскостью а и (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

3. Докажите, что в равнобедренном треугольнике биссектриса, проведенная к основанию, делит… Геометрия 7 класс А.П. Ершова. КП-3 Вариант А 2

3.
Докажите, что в равнобедренном треугольнике биссектриса, проведенная к основанию,
делит треугольник на два (Подробнее…)

ГДЗГеометрия7 классЕршова А.П.

Найдите: 4) косинус угла ВАС. Геометрия Зив Б.Г. 10 класс. Контрольные работы 6. Вариант 4

В равнобедренной трапеции ABCD с основаниями AD и
ВС диагонали АС и BD перпендикулярны. Средняя ли-
ния трапеции РК = 2,5. (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

1. Найти углы треугольника АВС. А.П. Ершова Геометрия 7 класс. СП-9 Вариант А 2

(Подробнее. ..)

ГДЗЕршова А.П.7 классГеометрия

2. В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD — квадрат… 10 класс Геометрия Зив Б.Г. Самостоятельная работа 12. Вариант 3

2.   В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD — квадрат, AD = 2, АС1 = 2√6.
1)  Найдите СС1.
2)  Докажите, (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

2. Дано окружность с центром О, ∆АВС — правильный… 10 класс Зив Б.Г. Геометрия. Повторение планиметрии 2. Вариант 7

(Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

2. Точки А, В и С лежат на одной прямой, причем АВ:ВС = т:п (не равные друг другу натуральные… Геометрия А.П. Ершова 7 класс. СП-4 Вариант 2.

2.
Точки А, В и С лежат на одной прямой,
причем АВ:ВС = т:п (не равные (Подробнее…)

ГДЗГеометрия7 классЕршова А.П.

похожие темы

Экскурсии

Мякишев Г. Я.

Досуг

Кузнецова Л. В.

Вопросы и решения по математике для 10 класса

The Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя ряд вопросов, улучшенных новыми технологиями.

Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Сопоставление таблиц, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнения / числа, Расширенный построенный ответ, Короткий ответ и многое другое. .

Эта страница содержит несколько примеров вопросов, а также ссылки на практические тесты по математике для 10 класса, которые дают вам представление о вопросах, которые ваши учащиеся, скорее всего, увидят в тесте. После каждого примерного вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, потребуется рассмотреть для навыков, процессов и информации, которые должны знать ваши студенты.

Сфера: 10 класс >> Число и количество – Система реальных чисел

Пример вопроса: Оценка 9 ^150/300

1. 18
2. 9
3. 3
4. 81

Объяснение ответа: 9 ^150/300 = 9 ^1/2 = квадратный корень из 9 = 3. В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени можно уменьшить, поэтому сначала мы должны уменьшить его. Показатель степени 150/300 = 1/2. Итак, проблема становится 9в 1/2 степени. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, что равно 3. Числитель равен 1, поэтому мы возводим 3 в первую степень, и ответ равен 3.

Стандарты: HSN.RN.A.1

Щелкните здесь, чтобы попрактиковаться: Число и количество – система действительных чисел Вопросы по математике 10 класса

Область: 10 класс >> Число и количество – количества

Пример вопроса: Перепишите x ^1/2 в радикальной форме.

1. √х
2. √x ²
3. 1/√x
4. -√x

Объяснение ответа: В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Поскольку проблема в том, x ^1/2 , знаменатель равен 2, что означает, что мы должны извлечь квадратный корень, а числитель равен 1, поэтому мы должны возвести это в первую степень, иначе не будет показателя степени, поскольку показатель степени 1 редко встречается. использовал. Таким образом, ответ представляет собой квадратный корень из x, записанный как √x.

. Стандарты: HSN.RN.A.1. Вопрос: Полностью упростить i(7−i)

1. 7i−i ²
2. 1+7i
3. 6и
4. −1+7i

Объяснение ответа: i(7−i)=i*7−i*i=7i−i ² =7i−(−1)=7i+1=1+7i

Начните с использования метода распределения. Теперь упростим -i ² =1 по определению. Теперь переставьте и поставьте действительную часть первой, а мнимую последней, чтобы она выглядела как a+bi.

Стандарты: HSN.CN.A.2

Нажмите здесь, чтобы попрактиковаться: 10 класс.

Пример вопроса: Вектор в стандартной форме имеет компоненты. Что такое начальная точка?

1. (0, 0)
2. (3, 10)
3. (6, 20)
4. Недостаточно информации

Ответ Объяснение: Поскольку вектор находится в стандартном положении, мы знаем, что начальная точка (0, 0) или начало координат.

Стандарты: HSN.VM.A.2

Нажмите здесь, чтобы потренироваться: Число и количество – векторные и матричные величины0012

Предмет: 10 класс >> Алгебра – Видение структуры в выражениях

Пример вопроса: Какое выражение эквивалентно 9x ² – 16y ² ?

1. (3x – 4 года) (3x – 4 года)
2. (3x + 4г) (3x + 4г)
3. (3x + 4 года) (3x – 4 года)
4. (3x – 4 года) ²

Объяснение ответа: Студент должен распознать выражение как разность двух полных квадратов

Стандарты: HSA. SSE.A.2

Нажмите здесь, чтобы попрактиковаться: Алгебра – Видение структуры в выражениях Вопросы по математике для 10 класса

Область: 10 класс >> Алгебра – арифметика с полиномами и рациональными выражениями

Пример вопроса: Вычислить f(x)=−a ³ +6a−7 при a = – 1 и указать остаток.

1. -14
2. -12
3. 14
4. 12

Объяснение ответа: студент должен подставить – 1 в функцию следующим образом −(−1) ³ +6(−1)−7=−12 и найти значение, чтобы получить остаток

Стандарты: HSA.APR.B. 2

Щелкните здесь для практики: Алгебра – арифметика с полиномами и рациональными выражениями Вопросы для 10 класса Математика

Предмет: 10 класс >> Алгебра – составление уравнений

Пример вопроса: Соотношение персонала и гостей в гала было 3 на 5. Всего в бальном зале было 576 человек. Сколько гостей было на гала?

1. 276
2. 300
3. 360
4. 216

Объяснение ответа: Установите пропорцию гостей к общему количеству людей, 8/5 = x/576.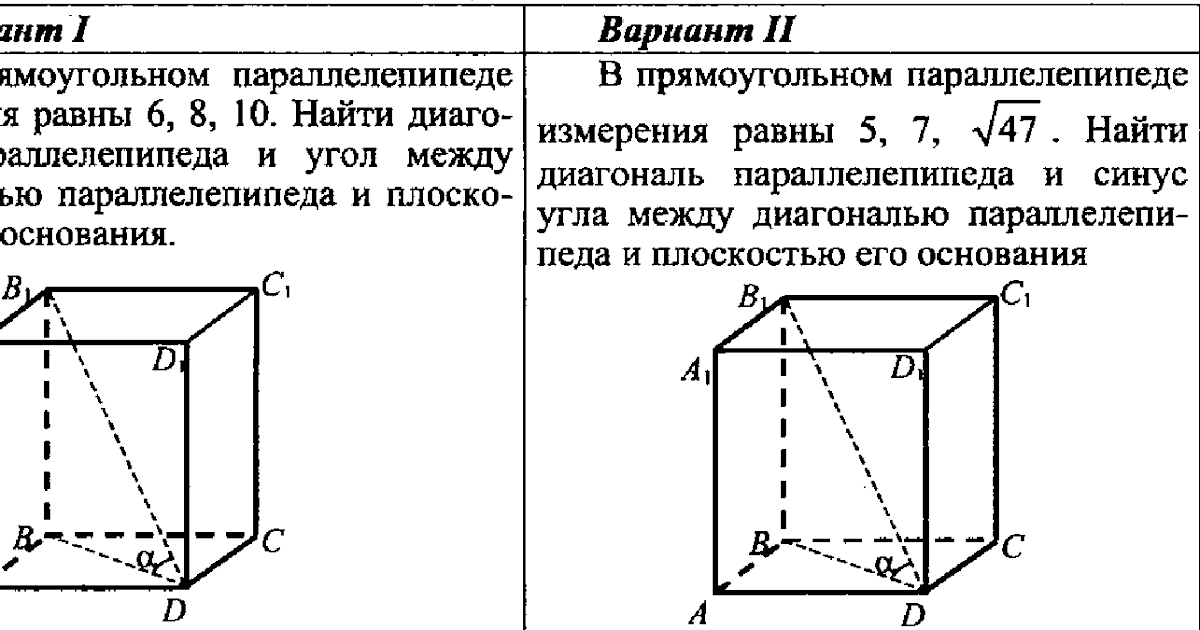 Решите перекрестным умножением. 8x = 2880. Разделите обе части на 8. Таким образом, x = 360.

. Стандарты: HSA.CED.A.3.0009

Пример вопроса: Решите квадратное уравнение x ² +10x=−25.

1. -10
2. 10
3. 5
4. -5

Объяснение ответа: Эту задачу можно легко решить, перестроив уравнение так, чтобы оно решалось относительно нуля, а затем разложить на множители, как показано:

x ² +10x=−25 25=0

(x+5)(x+5)=0

Поскольку оба коэффициента абсолютно одинаковы, у вас будет только одно решение этой проблемы.

x+5=0

x=−5

Стандарты: HSA.REI.B.4

Щелкните здесь, чтобы попрактиковаться: Алгебра – Рассуждения с помощью уравнений и неравенств. Вопросы для 10 класса по математике

83 Область знаний : 10 класс >> Функции – интерпретация функций

Пример вопроса: Какой график может представлять график функции f(x)=sin(x)?

Объяснение ответа: График функции sin всегда выглядит как волна.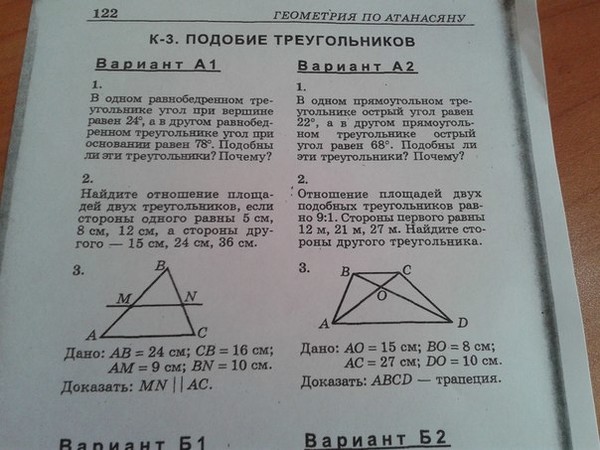 Функция sin может быть только D.

Стандарты: HSF.IF.C.7

Щелкните здесь, чтобы попрактиковаться: Функции – Интерпретация функций Вопросы для 10 класса по математике

Домен: 10 класс > > Функции – построение функций

Пример вопроса: Опишите, как график g(x)=x ³ – 5 может быть получен сдвигом f(x) = x ³ + 2.

1. Сдвиг вправо 7 единиц
2. Сдвиг влево 7 единиц
3. Сдвиг вверх на 7 единиц
4. Сдвиг вниз на 7 единиц

Объяснение ответа: Единственное, что изменилось в двух уравнениях, это точка пересечения с осью y, которая управляет сдвигом по вертикали (вверх или вниз). Чтобы получить график g(x), сдвинув график f(x), вы должны сдвинуть f(x) вниз на 7 единиц, чтобы измениться с +2 на -5.

Стандарты: HSF.BF.B.3

Нажмите здесь, чтобы потренироваться: Функции – Построение функций Вопросы для 10 класса Математика

Домен: 10 класс >> Функции – интерпретация функций

Пример вопроса: Решите 3 ^x =12, используя логарифмическую форму.

1. х = ln12/ln3
2. х = пер(4)
3. х = пер(9)
4. Ни один из этих

Объяснение ответа:
Решите с помощью журналов следующим образом:
3 ^x =12
x=log(основание 3) 12
x=ln12/ln3

Щелкните здесь, чтобы попрактиковаться: Функции — интерпретация функций Вопросы для 10 класса по математике

Область: 10 класс >> Функции — тригонометрические функции

Пример вопроса: В единичном круге видно, что tan(5π/4) =1 . Каково значение cos(5π/4)?

1. −√2/2
2. не определено
3. √2/2
4. -1

Объяснение ответа:
Тригонометрическое отношение косинуса равно отношению длины прилежащей стороны к длине гипотенузы. Длина смежной стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, соответствующей этому углу. Тригонометрическое отношение тангенса равно длине противолежащей стороны, деленной на длину прилежащей стороны. Длина противоположной стороны — это значение y в точке единичной окружности, а длина соседней стороны — это значение x в точке единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения тангенсов любого угла в единичной окружности — это отношение yx от точки на единичной окружности, соответствующей этому углу. В этом вопросе тангенс(5π/4)=1. Это отношение берется из точки (−2/√2, −2/√2), которая соответствует углу величиной 5π/4 радиана. Таким образом, используя приведенную выше информацию, значение cos(5π4) совпадает со значением x в точке (−2/√2, −2/√2). Следовательно, значение cos(5π/4) =-2/√2.

. Стандарты: HSF.TF.A.2. будут координатами точки S после применения следующего правила: (x+3, y -2)?

1. (1, -4)
2. (-2, -2)
3. (2, -2)
4. (3, -2)

Объяснение ответа: Ответ: B
Объяснение: Данное правило преобразования заключается в перемещении точки на 3 единицы вправо и на 2 единицы вниз, как показано на следующей диаграмме:

Стандарты:

Нажмите здесь, чтобы попрактиковаться: Геометрия – Вопросы на соответствие для 10 класса Математика

Область: 10 класс >> Геометрия – подобие, прямоугольные треугольники и тригонометрия

Пример вопроса: По какому свойству углы BAX и TSX могут быть признаны равными?

1. Соответствующие углы
2. Вертикальные уголки
3. Альтернативные внутренние углы
4. Равные углы

Объяснение ответа: Ответ: A

Несмотря на то, что они равны, вопрос задает свойство. Поскольку они находятся в соответствующих местах с поперечной (AX), правильный ответ: A

Стандарты: HSG.SRT.A.3

Нажмите здесь, чтобы попрактиковаться: Геометрия — подобие, прямоугольные треугольники и тригонометрия Вопросы для оценки 10 Математика

Домен: 10 класс >> Геометрия – Окружности

Пример вопроса: Каково правило перевода и масштабный коэффициент расширения, когда Окружность F→Окружность F′ ?

1. (x,y)→1/4(x,y+10)
2. (х, у)→4(х, у+10)
3. (х, у)→1/4(х+10,у)
4. (х, у) → 1/4 (х, у-10)

Ответ Объяснение: Исходный круг F имеет центр в точке (−5,−6) с радиусом 4 единицы. Перемещенный/расширенный круг F’ имеет центр в точке (−5,4) с радиусом 1 единица. Это означает, что центр был перемещен вверх на 10 единиц. В качестве преобразования этот перевод записывается как (x,y)→(x,y+10). Окружность F также расширилась в 1/4 раза, потому что радиус был уменьшен с 4 единиц до 1 единицы. В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Соединяя перевод и расширение вместе, правило (x, y) → 1/4 (x, y + 10).

Стандарты:

Щелкните здесь, чтобы попрактиковаться: Геометрия – круги Вопросы для 10 класса Математика

Область: 10 класс >> Геометрия – Выражение геометрических свойств с помощью уравнений

Пример1 Вопрос 2: 900 Число 1 линия на рисунке ниже делит отрезок EF на две части с отношением их длин 3:1?

1. -5
2. -3
3. -2
4. -1

Объяснение ответа: На числовой прямой на рисунке точка E находится в точке -7, а точка F в точке 1. Таким образом, длина отрезка EF равна 8. Разделить отрезок на две части с отношением их длин 3:1, измените соотношение на 3x:1x, чтобы разрешить изменение положения на числовой прямой. Затем установите сумму двух частей равной 8 и найдите x. 3x+1x=8;4x=8;x=2. Теперь, когда вы знаете, что x=2, найдите 3x, равное 6. Найдите значение на числовой прямой, прибавив 6 к позиции точки E. −7 +6=-1. Значение на числовой прямой, которая делит отрезок EF в отношении 3:1, равно -1.

Стандарты: HSG.GPE.B.6

Нажмите здесь, чтобы попрактиковаться: Геометрия – Выражение геометрических свойств с помощью уравнений Пример вопроса: Каков объем показанной ниже призмы?

1. 1350 см ³
2. 1350 см
3. 675 см ³
4. 675 см

Объяснение ответа: Используйте формулу объема пирамиды:

V=1/2.a.c.h

В этом случае длина 15см, длина основания 10см, высота 9см. Следовательно:

V=1/2.15.10.9=675 см ³

Стандарты: HSG.GMD.A.3

Нажмите здесь, чтобы попрактиковаться: Геометрия – геометрические измерения и размеры Вопросы для 901 класса

Математика

Домен: 10 класс >> Геометрия – Моделирование с помощью геометрии

Пример вопроса: Компания отправляет сферические пресс-папье в кубических коробках. Окружность пресс-папье 9π см. Если коробка соответствует сфере точно так, что стороны сферы касаются коробки, каков объем наименьшей коробки, которую компания может использовать для доставки?

1. 81 см ³
2. 81 см ³
3. 729 см ³
4. 1009 π см ³

Объяснение ответа:

Обратите внимание, что диаметр сферы будет таким же, как сторона куба. Используя значение окружности, можно определить диаметр пресс-папье.
C = πd9π
см = πd9
см = d
Так как диаметр равен сторонам {\dots}
V=s ³
V=(9 см) ³
V=729 см ³

Стандарты: HSG.MG.A.3

Нажмите здесь для практики: Геометрия – Моделирование с помощью геометрии Вопросы для 10 класса Математика

Область: 10 класс >> Статистика и вероятность – интерпретация категориальных и количественных данных

Пример вопроса: Какой тип функции, представленной ниже, показывает корреляцию между двумя переменными?

1. Линейный
2. Экспоненциальный
3. Квадратичный
4. Полярный

Ответ Объяснение: Обратите внимание, что тренд графика (красный) между точками данных образует линию.

Стандарты: HSS.ID.A.4

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – интерпретация категориальных и количественных данных. & Обоснование выводов

Пример вопроса: В исследовательском проекте о поведении домашних животных была выбрана случайная выборка из 400 кошек. Исследование показало, что 60% кошек предпочитают спать внутри дома. Курица была любимой едой для 35% этих кошек. Исследование также показало, что у 85% кошек, которые предпочитали спать вне дома, было другое любимое блюдо. Сколько кошек в выборке больше всего любили курицу и предпочитали спать внутри?

1. 84
2. 56
3. 160
4. 156

Объяснение ответа: Если в выборке 400 кошек и 60% кошек предпочитают спать внутри, то 400.0.60=240 кошек предпочитают спать внутри, а 160 кошек предпочитают спать снаружи. Далее, если любимым блюдом 35% тех кошек, которые предпочли спать внутри, была курица, то 240,0,35=84 кошки в выборке предпочли спать внутри и имели курицу в качестве своего любимого блюда.

Стандарты: HSS.IC.B.6

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – выводы и обоснование выводов Правила вероятности

Пример вопроса: В студенческом совете есть одна предстоящая вакансия. Школа проводит выборы и имеет восемь равновероятных кандидатов. Класс статистики AP хочет смоделировать результаты выборов, поэтому учащиеся должны выбрать подходящий метод моделирования. Они намерены провести испытания с симуляцией. Какой из этих методов будет наиболее подходящим?

1. Вращение колеса с восемью равными ячейками
2. Подбросьте монету восемь раз за каждые выборы
3. Бросить кости
4. Бросьте четыре кубика

Объяснение ответа: В вопросе говорится, что существует восемь равновероятных кандидатов. Это означает, что каждый кандидат имеет одинаковые шансы на победу на выборах. Только вращающееся колесо с восемью равными ячейками может имитировать эту ситуацию, потому что у колеса есть равные шансы приземлиться на каждой ячейке.

Стандарты: HSS.IC.A.1

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Условная вероятность и правила вероятности Вопросы для 10 класса по математике Использование вероятности для принятия решений

Пример вопроса:

Используя приведенную выше диаграмму Венна, найдите P(C или E).

1. 1/3
2. 7/24
3. 5/24
4. Ни один из этих

Ответ Объяснение: Просто подсчитайте точки данных в кругах C и E. Их 8 из 24 общих точек данных, и, уменьшая, мы получаем 8/24=1/3.

Стандарты: HSS.CP.B.7

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Использование вероятности для принятия решений Вопросы для 10 класса по математике принимать решения

Пример вопроса: Статистик, работающий в Sweet Shop USA, получил задание выяснить, какова вероятность того, что аппарат для помадки выйдет из строя и в процессе работы будет испорчена целая партия помадки.