Геометрия дидактические материалы 10 класс зив гдз: ГДЗ решебник по геометрии 10 класс Зив дидактические материалы

• ГДЗ
• 1 КЛАСС
  • Английский язык
  • Русский язык
  • Математика
  • Окружающий мир
  • Литература
  • Информатика
  • Музыка
  • Человек и мир
  • Технология
• 2 КЛАСС
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Математика
  • Окружающий мир
  • Литература
  • Белорусский язык
  • Информатика
  • Музыка
  • Человек и мир
  • Французский язык
  • Технология
  • Испанский язык
• 3 КЛАСС
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Математика
  • Окружающий мир
  • Литература
  • Белорусский язык
  • Информатика
  • Музыка
  • Человек и мир
  • Французский язык
  • Технология
  • Испанский язык
  • Казахский язык
• 4 КЛАСС

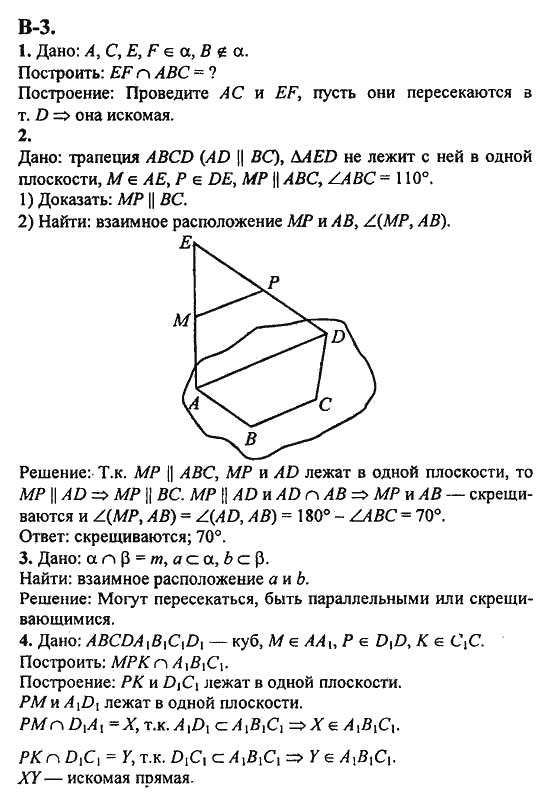
ГДЗ / Дидактические материалы по геометрии 10 класс / Зив Б. Г. / 2009 — 18 Февраля 2017

Аннотация: 4-е изд., перераб. и испр. — М.: 2009, 254 с.
Решение контрольных и самостоятельных работ по геометрии за 11 класс к пособию «Дидактические материалы по геометрии для 10 класса» Зив Б.Г.

ГДЗ по геометрии, 10 класс, Попов М.А., 2009, к учебнику по геометрии за 10 класс, Зив Б.Г., 2007.

  Предлагаемое учебное пособие содержит подробное решение всех заданий самостоятельных и контрольных работ из пособия «Геометрия: дидактические материалы для 10 класса».
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии.

Примеры.
В наклонном параллелепипеде основанием служит квадрат. Две противоположные боковые грани перпендикулярны к плоскости основания. Все ребра параллелепипеда равны между собой. Площадь наклонной боковой грани равна 25 см2. Длина ребра параллелепипеда равна….
Решение: 5.

В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 50°. Угол между противоположными боковыми гранями пирамиды равен … .
Решение: (180-50°•2) = 80°.

Содержание
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
ВАРИАНТ 1 5
ВАРИАНТ 2 20
ВАРИАНТ 3 33
ВАРИАНТ4 48
ВАРИАНТ 5 64
ВАРИАНТ 6 87
ВАРИАНТ 7 104
ВАРИАНТ 8 122
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ НА ПОВТОРЕНИЕ ПЛАНИМЕТРИИ
СП-1 156
СП-2 171
ДОПОЛНИТЕЛЬНЫЕ САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
ДС-1
В-1 189
В-2 189
В-3 190
В-4 190
В-5 191
В-6 192
ДС-2
В-1 193
В-2 194
В-3 195
В-4 196
В-5 197
В-6 198
КОНТРОЛЬНЫЕ РАБОТЫ К-1
В-1 200
В-2 201
В-3 203
В-4 204
К-2
В-1 205
В-2 207
В-3 210
В-4 212
к-3
В-1 214
В-2 215
В-3 217
В-4 219
К-4
В-1 220
В-2 222
В-3 224
В-4 226
К-5
В-1 228
В-2 229
В-3 231
В-4 233
К-6
В-1 234
В-2 236
В-3 237
В-4 239
МАТЕМАТИЧЕСКИЕ ДИКТАНТЫ МД-1
В-1 243
В-2 244
МД-2
В-1 246
В-2 247
мд-3
В-1 249
В-2 250
МД-4
В-1 251
В-2 252.

Дидактический материал по Геометрии 10 класс.

Математические диктанты по геометрии

10 класс

Аксиомы стереометрии

1. Запишите основные фигуры стереометрии.

2. Постройте плоскость α, прямую СД, лежащую в данной плоскости и точку А, не лежащую в плоскости. Сделайте соответствующие записи.

3. Верно ли, что: а) любые три точки лежат в одной плоскости; б) через любые три точки проходит плоскость и притом только одна.

4. Верно ли, что прямая лежит в плоскости треугольника, если она пересекает две стороны треугольника?

5. Закончите предложение: Если две плоскости имеют общую точку, то они…

6. Можно ли через точку пересечения двух прямых провести третью прямую, не лежащую с ними в одной плоскости?

7. Верно ли, что если две точки окружности лежат в одной плоскости, то и вся окружность лежит в этой плоскости?

8. Два диаметра окружности принадлежат одной плоскости. Принадлежит ли вся окружность этой плоскости?

9. Могут ли прямая и плоскость иметь только одну общую точку? Только две общие точки?

Диктант «Аксиомы стереометрии»

1. Сформулируйте аксиому стереометрии С₁.

2. Заполните пропуски, чтобы получилось верное утверждение:

а) Через прямую и не лежащую на ней точку можно провести ________________________ и притом только одну;

б) Если А  а, а  α, то А … α.

3. «Да» и «нет» не говорите, лучше сразу напишите

а) Могут ли прямая и плоскость иметь только одну общую точку?

б) Могут ли прямая и плоскость иметь только две общие точки?

в) Можно ли через любые три точки провести единственную плоскость?

4. Верны ли следующие утверждения:

а) Если прямая пересекает две смежные стороны квадрата, то она лежит в плоскости этого квадрата.

б) Если две точки окружности лежат в одной плоскости, то и вся окружность лежит в этой плоскости.

в) Если две противоположные вершины параллелограмма лежат в одной плоскости, то и весь параллелограмм лежит в этой плоскости.

г) Если две прямые пересекаются в точке А, то все прямые, не проходящие через точку А и пересекающие данные прямые, лежат в одной плоскости

Диктант «Взаимное расположение прямых»

1. Закончите предложения:

а) Две прямые в пространстве называются параллельными, если ________________________________________________________ .

б) Две прямые называются скрещивающимися, если ________________________________________________________ .

2. Заполните пропуски, чтобы получилось верное утверждение:

а) Две пересекающиеся прямые лежат в _______________ плоскости;

б) Если прямые а и в имеют две общую точку, то они ___________________ .

в) Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые _______________________________ .

г) Через точку пересечения двух данных прямых можно провести третью ______________________ , не лежащую с ними в одной плоскости.

д) Если прямая пересекает две пересекающиеся прямые и не проходит через точку их пересечения, то она лежит в ________________________ этих прямых.

3. Прямые а и b параллельны. Прямая с пересекает прямую а, но не пересекает b. Как расположены прямые с и b?

4. «Да» и «нет» не говорите, лучше сразу напишите

а) Прямые c и d принадлежат плоскости β. Могут ли прямые c и d быть параллельными?

б) Прямые а и b принадлежат одной плоскости. Могут ли эти прямые пересекаться?

Диктант «Параллельные прямые в пространстве. Параллельность прямой и плоскости»

1. Закончите предложения:

а) Признак параллельности прямых в пространстве _________________________________________________ .

б) Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом __________________________ .

в) Прямая и плоскость называются параллельными, если ___________________________________________________________ .

2. Известно, что две прямые с и d параллельны прямой к. Как взаимно расположены прямые с и d?

3. Через концы отрезка МN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках М_1, N₁ и К₁. Найдите длину отрезка КК₁, если отрезок МN не пересекает α и ММ₁ = 6 см, NN₁=2 см.

4. Прямые а и b не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и b?

5. Сколько можно провести через данную точку прямых, параллельных данной плоскости?

6. Две прямые параллельны некоторой плоскости. Могут ли эти прямые быть скрещивающимися?

7. Сторона АВ параллелограмма АВСD принадлежит плоскости α. Как расположены по отношению к плоскости α остальные стороны?

8. Прямые а и b – параллельны. Прямая а не лежит в плоскости α, прямая b принадлежит α. Какое взаимное расположение прямой а и плоскости α?

Параллельные прямые в пространстве.

Параллельность прямой и плоскости

1. Всегда ли две непересекающиеся прямые в пространстве параллельны?

2. Всегда ли через две параллельные прямые можно провести плоскость?

3. Каким может быть взаимное расположение прямой и плоскости?

4. Верно ли, что если прямая, не лежащая в плоскости, параллельна ей, то она параллельная любой прямой, лежащей в этой плоскости?

5. Сколько можно провести через данную точку прямых, параллельных данной плоскости?

6. Две прямые параллельны некоторой плоскости. Могут ли эти прямые а) пересекаться? б) быть скрещивающимися?

7. Три вершины ромба лежат в плоскости. Принадлежит ли этой плоскости четвертая вершина ромба?

8. Средняя линия трапеции лежит в некоторой плоскости. Пересекают ли основания трапеции эту плоскость?

9. Сколько можно провести через данную точку прямых, параллельных данной плоскости?

10. Две смежные стороны параллелограмма пересекают плоскость. Пересекают ли эту плоскость две другие стороны параллелограмма?

Диктант 4 «Параллельность плоскостей»

1. Закончите предложения:

а) Две плоскости называются параллельными, если _________________.

б) Признак параллельности плоскостей:__________________________ .

2. Сколько случаев взаимного расположения плоскостей в пространстве и какие?

3. Будут ли параллельны плоскости, если прямая, лежащая в одной плоскости, параллельна другой плоскости?

4. Будут ли параллельны плоскости, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

5. Каким может быть взаимное расположение прямых а и b, каждая из которых лежит в одной из параллельных плоскостей?

6. Заполните пропуски, чтобы получилось верное утверждение:

а) Если одна из противоположных сторон параллелограмма пересекает плоскость α, то и другая сторона ________________________ эту плоскость.

б) Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом ___________________________ .

в) Противоположные грани куба лежат в _________________ плоскостях.

г) Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями ____________________________ .

Параллельные плоскости

1. Закончите предложение: Две плоскости называются параллельными, если…

2. Верно ли, что две плоскости параллельны, если две прямые, лежащие в одной плоскости, параллельные двум прямым, лежащим в другой плоскости?

3. Сформулируйте Аксиому 3.

4. Верно ли, что если две стороны треугольника параллельны плоскости, то и третья сторона параллельна этой плоскости?

5. Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции?

6. Как называются вершины параллелепипеда, не принадлежащие одной грани?

7. Какие фигуры являются гранями параллелепипеда?

8. Постройте сечение тетраэдра плоскостью, проходящей черед данные точки.

Диктант «Перпендикулярность прямых и плоскостей»

1. Заполните пропуски, чтобы получилось верное утверждение:

а) Две прямые называются перпендикулярными, если ________________ .

б) Прямая и плоскость называются перпендикулярными, если __________ .

в) Две прямые, перпендикулярные одной и той же плоскости __________________________________________ .

г) Если две плоскости перпендикуляры прямой, то они ________________ .

2. Сколько перпендикуляров можно провести через данную точку к данной прямой на плоскости?

3. Сколько перпендикуляров можно провести через данную точку к данной прямой в пространстве?

4. Прямые а и b – пересекаются. При каком условии можно провести через а плоскость, перпендикулярную b?

5.Прямая проходит через вершину А треугольника АВС перпендикулярно сторонам АВ и АС. Как она расположена относительно стороны ВС?

2. Вставьте пропущенное слово

а) Если плоскость перпендикулярна одной из двух параллельных прямых, то она _________________________________________ и другой.

б) Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая ________________________ этой плоскости.

Диктант «Перпендикулярность и наклонная.

Теорема о 3 перпендикулярах»

1. Закончите предложения:

а) Перпендикуляром, опущенным из данной точки на данную плоскость, называется__________________________________________________ .

б) Основанием перпендикуляра называется _________________________ .

в) Расстоянием между прямой и плоскостью называется ____________________ .

г) Наклонной, проведенной из данной точки к данной плоскости, называется ____________________________________________________ .

д) Основанием наклонной называется ______________________________ .

е) Проекцией наклонной на плоскость называется _____________________ .

ж) Теорема о трех перпендикулярах: ________________________________ .

2. Может ли наклонная быть короче перпендикуляра, проведенного из той же точки и к той же плоскости?

3. Если наклонные, проведенные из одной точки к плоскости равны, то что можно сказать об их проекциях?

4. Точка А не лежит в плоскости α. Сколько наклонных заданной длины можно провести из этой точки к данной плоскости?

Диктант 7 «Перпендикулярность плоскостей»

1. Закончите предложения:

а) Две пересекающиеся плоскости называются перпендикулярными, если ________________________________ .

б) Признак перпендикулярности двух плоскостей: _____________________ .

в) Две смежные грани прямоугольного параллелепипеда лежат в _______________________________ плоскостях.

г) Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна их линии пересечения, то она перпендикулярна и другой__________________________________________ .

д) Плоскость, перпендикулярная прямой, по которой пересекаются две данные плоскости, перпендикулярна каждой из этих ________________ .

е) В прямоугольном параллелепипеде все шесть граней ________________ .

ж) Длины ребер прямоугольного параллелепипеда, имеющие общую вершину, называются ___________________________________ .

2. Сколько можно провести плоскостей через данную точку, перпендикулярных данной плоскости?

3. Сколько существует плоскостей, проходящих через данную прямую (не перпендикулярную плоскости) и перпендикулярных данной плоскости?

4. Прямые а и b – параллельные и лежат в плоскости α. Через каждую из этих прямых проведена плоскость, перпендикулярная α. Каково взаимное расположение полученных плоскостей?

Перпендикулярность прямой и плоскости

1. Закончите предложение: а)Прямая называется перпендикулярной к плоскости, если … б) Если плоскость перпендикулярна к одной из двух параллельных прямых, то она…

2. Закончите предложение: Две прямые, перпендикулярные одной и той же плоскости …

3. Можно ли утверждать, что прямая, проходящая через центр круга перпендикулярно диаметру, перпендикулярна плоскости круга?

4. Можно ли утверждать, что прямая перпендикулярна плоскости, если она перпендикулярна лежащим в этой плоскости двум сторонам квадрата; двум сторонам треугольника?

5. Закончите предложение: если одна из двух параллельных прямых перпендикулярна плоскости, то …

6. Установите взаимное положение прямых а и b

7. Запишите теорему, обратную теореме о трёх перпендикулярах.

Многогранники

1. Запишите известные вам многогранники.

2. Равны ли многоугольники, лежащие в основаниях призмы?

3. Какими фигурами являются боковые грани призмы?

4. Что называется кубом?

5. Призма имеет 30 граней. Какой многоугольник лежит в её основании?

6. Закончите предложение: Призма называется прямой, если…

7. Может ли быть наклонной призма, основанием которой является прямоугольник?

8. Что называется апофемой пирамиды?

9. Чему равна площадь боковой поверхности правильной пирамиды?

10. Боковые рёбра пирамиды равны между собой. Может ли основанием пирамиды быть ромб? Прямоугольник?

11. Боковые рёбра пирамиды равны между собой. Как расположена проекция вершины пирамиды на основание, если основание прямоугольник? Прямоугольный треугольник?

Параллельность прямой и плоскости».

1. Могут ли две различные прямые в пространстве иметь более одной общей точки? (Пояснить)

2. Могут ли вершины замкнутой ломаной линии, состоящей из 4 звеньев, не принадлежать одной плоскости? (Пояснить)

3. Прямые a и b параллельны плоскости α. Укажите взаимное положение этих прямых.

4. Плоскости α и β пересекаются по прямой m. Прямая a параллельна плоскости α и плоскости β. Каково взаимное положение прямых a и m?

5. Верно ли утверждение: если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

Математический диктант. (Геом.10кл.урок 13-14)

1. Верно ли утверждение , что если прямая , не лежащая в плоскости , параллельна ей , то она параллельна любой прямой , лежащей в этой плоскости .

2. Верно ли утверждение , что если две прямые параллельны одной и той же плоскости , то они параллельны между собой .

3. Каким может быть взаимное расположение двух прямых , из которых одна параллеьна некоторой плоскости , а другая пересекает эту плоскость.

4. Верно ли утверждение параллельности прямой и плоскости “Прямая , параллельная какой либо прямой на плоскости , параллельна и самой плоскости “.

5. Прямые а и в параллельны . Какой положение может занимать прямая а относительно плоскости , проходящей через прямую в .

6. Одна из двух параллельных прямых параллельна некоторой плоскости . Можно ли утверждать , что и вторая прямая параллельна этой плоскости .

7. Даны две пересекающие плоскости . Существует ли плоскость , пересекающая две данные плоскости по параллельным прямым.

8. Верно ли утверждение : если две прямые не имеют общих точек , то они параллельны .

9. Две прямые параллельны некоторой плоскости . Могут ли эти прямые

а) пересекаться б) быть скрещивающимися

10. Могут ли скрещивающиеся прямые а и в быть параллельными прямой с .

11. Даны две скрещивающиеся прямые а и в . Точки А и А₁ лежат на прямой а , точки В и В₁ лежат на прямой в . Как будут расположены прямые АВ и А₁В_{1 .}

12. Прямая а скрещивается с прямой в , а прямая в скрещивается с прямой с . Следует ли из этого , что прямые а и с скрещиваются .

13. Каково должны быть взаимное расположение трех прямых , чтобы можно провести плоскость , содержащую все прямые .

Математический диктант

1. Какие две прямые в пространстве называются параллельными

2. Сформулируйте признак параллельности прямой и плоскости

3. Дан куб АВСДА₁В₁С₁Д₁. назовите четыре пары параллельных прямых , четыре пары пересекающих прямых.

4. Какие возможны случаи взаимного расположения прямой и плоскости.

5. Верно ли утверждение :если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость .

Математический диктант

1. Могут ли прямая и плоскость не иметь общих точек?

2. Верно ли, что если две прямые не пересекаются, то они параллельны?

3. Плоскости α и β параллельны , прямая m лежит в плоскости α. Верно ли , что прямая m параллельна плоскости β?

4. Верно ли , что если прямая m параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая mимеет только одну общую точку?

5. Верно ли, что боковые стороны трапеции параллельны плоскости α и плоскости трапеции?

6. Верно ли, что плоскости параллельны , если прямая лежащая в одной плоскости , параллельна другой плоскости?

7. Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей?

8. Верно ли, что любые четыре точки лежат в одной плоскости?

9. Верно ли , что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельны плоскости α?

Диктант Векторы в пространстве

1. Что называется вектором в пространстве? (Что такое модуль вектора?)

2. Какие векторы называются противоположно направленными (коллинеарными)?

3. Что называется суммой векторов х и у ? (Что называется скалярным произведением вектора х и вектора у?)

4. Как записать в координатах условие равенства вектора а и b? (Как определяется произведение вектора а на число ?)

5. Какие векторы называются равными? (Запишите условие перпендикулярности векторов.)

6. Что такое абсолютная величина вектора? (Каково направление нулевого вектора?)

7. Найдите сумму вектора х (1; -4; -5) и вектора у (3; 4; -5). (Найдите произведение числа – 3 на вектор b (4; 3; 10).)

8. Каковы координаты вектора с началом в точке (3; 2; -5) и концом в точке (-5; 2; 3;)? (Найдите координаты вектора, противоположного вектору b (7; 8; 9).)

9. Найдите скалярное произведение вектора а (1; 31; 2) и вектора b (-1; 0; 3)).

Векторы в пространстве

Вариант 1

1. Вектором в пространстве называется …

2. Вектор обозначается …

3. Длиной вектора называется …

4. Два вектора в пространстве называются одинаково направленными, если …

5. Для того, чтобы сложить два вектора, нужно

Вариант 2

1. Вектором на плоскости называется …

2. Вектор изображается …

3. Модулем вектора называется …

4. Два вектора в пространстве называются противоположно направленными, если …

5. При умножении вектора на число …

Диктант Углы между прямыми и плоскостями

1. Чему равен угол между прямой и параллельной ей плоскостью? (Чему равен угол прямой и пересекающей ее плоскостью?)

2. Чему равен угол между пересекающими плоскостями? (Чему равен угол между скрещивающимися прямыми?)

3. Что называется углом между скрещивающимися прямыми? (Что называется углом между двумя прямыми?)

4. Чему равен угол между параллельными плоскостями? (Чему равен угол между параллельными прямыми?)

5. Что называется углом между прямой и плоскостью? (Чему равен угол между двумя пересекающимися прямыми?)

6. Что называется углом между плоскостями? (Чему равен угол между перпендикулярными прямыми?)

7. В кубе А…D покажите угол между гранью ВВ С и диагональю АС (между плоскостью АВС и прямой ВD).

8. В кубе А…D покажите угол между пересекающимися плоскостями (между скрещивающимися прямыми).

Диктант Перпендикуляр и наклонная.

1. Сформулируйте условие теоремы о трех перпендикулярах (заключение теоремы о трех перпендикулярах).

2. Дайте определение перпендикуляра к плоскости (определение наклонной к плоскости).

3. Дайте определение проекции наклонной (перпендикулярной плоскостей).

4. Сформулируйте признак перпендикулярности плоскости. (Что называется основанием наклонной?)

5. Что называется расстоянием от прямой до параллельной ей плоскости? (Что называется основанием перпендикуляра?)

6. Что называется расстоянием между параллельными плоскостями? (Сформулируйте признак перпендикулярности плоскостей.)

7. Покажите на рисунке угол между проекцией наклонной и прямой, проведенной через основание наклонной (угол между наклонной и прямой, проведенной через основание наклонной).

8. Сделайте рисунок к теореме о трех перпендикулярах (к обратной теореме о трех перпендикулярах).

Диктант Свойства перпендикулярных прямой и плоскости.

1. Дайте определение прямой, перпендикулярной плоскости. (Какие прямые в пространстве называются перпендикулярными?)

2. Сколько прямых, перпендикулярных плоскости, можно провести через любую точку плоскости? (Что можно сказать о нескольких перпендикулярах к одной плоскости?)

3. Сколько плоскостей, перпендикулярных данной прямой, можно провести через точку вне данной прямой? (Сколько прямых, перпендикулярных плоскости, можно провести через точку, не лежащую в данной плоскости?)

4. Что можно сказать о прямой, параллельной перпендикуляру к плоскости? (Сколько плоскостей, перпендикулярных данной прямой, можно провести через точку вне данной прямой?)

5. Постройте прямую, перпендикулярную плоскости. (Постройте через данной прямой перпендикулярную ей плоскость.)

6. Постройте в пространстве три проходящие через одну точку взаимно перпендикулярные прямые. (Постройте через точку плоскости прямую, перпендикулярную плоскости.)

Диктант «Углы в пространстве»

1. Закончите предложения:

а) Углом между скрещивающимися прямыми называется угол между __________________________________________ .

б) Углом между прямой и плоскостью называется угол между этой прямой и ____________________________________________________ .

2. Ответьте на вопросы

а) Чему равен угол между параллельными прямыми?

б) В каком случае скрещивающиеся прямые перпендикулярны?

в) Что называется проекцией наклонной на плоскость?

г) Чему равен угол между параллельными плоскостями?

3. Справедливо ли утверждение?

а) Любая прямая на плоскости, перпендикулярная проекции наклонной, перпендикулярна и наклонной.

б) Плоскость, пересекающая параллельные плоскости, пересекает их под равными углами.

в) Прямая, проходящая через центр круга, перпендикулярна диаметру.

4. Точка А отстоит от плоскости на расстоянии 12см. Найдите длины наклонных, проведенных из этой точки, если они образуют с плоскостью углы 30⁰.

Диктант Пространственные фигуры

Вариант 1

1. Гранями многогранника называются …

2. Вершинами многогранника называются …

3. Куб – многогранник, у которого …

4. Прямая призма – призма, у которой …

5. Правильная пирамида – пирамида, у которой …

Вариант 2

1. Ребрами многогранника называются …

2. Диагоналями многогранника называются …

3. Параллелепипед – многогранник, у которого …

4. Пирамида – многогранник, у которого …

5. Правильная призма – призма, у которой …

Диктант Моделирование многогранников

Вариант 1

1. Развертка многогранника – это …

2. Для удобства склейки развертку многогранника нужно …

3. Развертка прямого параллелепипеда состоит из …

4. Развертка треугольной призмы состоит из …

5. Развертка правильной шестиугольной пирамиды состоит из …

Вариант 2

1. Чтобы получить развертку многогранника нужно …

2. Геометрический конструктор состоит из …

3. Развертка прямого параллелепипеда состоит из …

4. Развертка прямой пятиугольной призмы состоит из …

5. Развертка правильной четырехугольной пирамиды состоит из …

Диктант Скрещивающиеся прямые

Вариант 1

1. Две прямые в пространстве называются скрещивающимися, если …

2. Два отрезка называются скрещивающимися, если …

3. В тетраэдре имеется … пар скрещивающихся ребер.

4. Через точку, принадлежащую прямой, можно провести … прямых, скрещивающихся с этой прямой.

5. Даны две скрещивающиеся прямые и третья прямая, их пересекающая. Плоскости, проходящие через первую и третью прямые и через вторую и третью прямые …

Вариант 2

1. Две прямые в пространстве называются параллельными, если …

2. Две прямые в пространстве скрещиваются, если они не пересекаются и …

3. Две прямые скрещиваются, если одна из них лежит в плоскости, а другая …

4. Через точку, не принадлежащую прямой, можно провести … прямых, скрещивающихся с этой прямой.

5. В четырехугольной пирамиде имеется … пар скрещивающихся ребер.

11:11. ..

()

.. —

1
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp17 2
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp18 & nbsp19 & nbsp19 3
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp18 & nbsp19 & nbsp19 4
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp18 & nbsp19 & nbsp19 5
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp19 & nbsp
6
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp18 & nbsp19 & nbsp
7
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp18 & nbsp19 & nbsp19 8
1 & nbsp2 & nbsp3 & nbsp4 & nbsp5 & nbsp6 & nbsp7 & nbsp8 & nbsp9 & nbsp10 & nbsp11 & nbsp12 & nbsp13 & nbsp14 & nbsp15 & nbsp16 & nbsp17 & nbsp18
-1
1 & nbsp2 & nbsp3 & nbsp4
-2
1 & nbsp2 & nbsp3 & nbsp4
-3
1 & nbsp2 & nbsp3 & nbsp4
-4
1 & nbsp2 & nbsp3 & nbsp4
К-1
1 & nbsp2 & nbsp3 & nbsp4
К-2
1 & nbsp2 & nbsp3 & nbsp4
К-3
1 & nbsp2 & nbsp3 & nbsp4
К-4
1 & nbsp2 & nbsp3 & nbsp4



CBSE Class 10 Maths MCQ по координатной геометрии PDF

Мы предоставляем здесь вопросы с множественным выбором типов (MCQ) по CBSE Class 10 Maths, Глава 7: Координатная геометрия.Все эти вопросы предназначены для того, чтобы помочь студентам легко пересмотреть важные фундаментальные концепции для подготовки вопросов объективного типа к экзамену CBSE Class 10 по математике 2021 года. Здесь вы также получите точные ответы на все вопросы с подробным решением / объяснением.

Примечание — Студенты должны отметить, что « Площадь треугольника» исключена из пересмотренной программы CBSE по математике 10 класса . Таким образом, студенты должны готовиться только по новой программе.

Проверьте ниже решенные MCQ по математике класса 10 Глава 7 Координатная геометрия:

1. Если расстояние между точками (2, –2) и (–1, x) равно 5, одно из значений x равно

(А) –2

(В) 2

(К) –1

(Д) 1

Ответ: (B)

Пояснение: Согласно вопросу

2. Средняя точка отрезка прямой, соединяющего точки A (–2, 8) и B (- 6, — 4), равна

.

(А) (- 4, — 6)

(В) (2, 6)

(К) (- 4, 2)

(Д) (4, 2)

Ответ: (C)

Пояснение: Пусть координаты средней точки будут (x, y), тогда

Следовательно, координаты

3. Точки A (9, 0), B (9, 6), C (–9, 6) и D (–9, 0) являются вершинами

(А) Площадь

(B) Прямоугольник

(C) Ромб

(D) Трапеция

Ответ: (B)

Пояснение: Здесь мы вычислим размеры всех четырех сторон четырехугольника, образованного заданными точками A, B, C и D.

Так как, AB = CD и BC = AD

Следовательно, данные точки A, B, C и D являются вершинами прямоугольника.

4. Расстояние точки P (2, 3) от оси x равно

(А) 2

(В) 3

(К) 1

(Г) 5

Ответ: (B)

Пояснение: Расстояние точки P (2, 3) от оси X = Ордината точки (2, 3), т.е. 3.

5 . Расстояние между точками A (0, 6) и B (0, –2) составляет

(А) 6

(В) 8

(К) 4

(Д) 2

Ответ: (B)

Пояснение: Здесь x ₁ = 0, y ₁ = 6, x ₂ = 0, y ₂ = –2

6. AOBC — это прямоугольник, три вершины которого — вершины A (0, 3), O (0, 0) и B (5, 0). Длина его диагонали

.

(А) 5

(В) 3

(К) √34

(Д) 4

Ответ: (C)

Пояснение:

Длина диагонали — это расстояние между точками AB.

Расстояние рассчитывается как,

7. Если P (a / 3, 4) — это средняя точка отрезка прямой, соединяющего точки Q (- 6, 5) и R (- 2, 3), то значение a равно

.

(А) — 4

(В) — 12

(К) 12

(Д) — 6

Ответ: (B)

Пояснение: As (a / 3, 4) — это середина отрезка прямой, соединяющего точки Q (- 6, 5) и R (- 2, 3) . Следовательно,

8. Координаты точки, которая равноудалена от трех вершин Δ AOB, как показано на рисунке:

(А) (х, у)

(В) (у, х)

(К) (х / 2, у / 2)

(Д) (у / 2, х / 2)

Ответ: (A )

Пояснение: Поскольку мы должны найти координаты, которые равноудалены от A и B, пусть точки будут (a, b).

Тогда (a, b) будет серединой AB.

Следовательно,

Следовательно, координаты (x, y)

9. Окружность, начерченная через центр, проходящую через Точку, которая не лежит внутри круга, —

(К) (5, –1/2)

(D) (–6, 5/2)

Ответ: (D)

Пояснение: Если точка лежит внутри круга, расстояние от центра до точки должно быть меньше радиуса окружности.

Радиус круга — это расстояние между началом координат и точкой

Расстояние между исходной точкой и (-3/4, 1) равно

Аналогично, расстояние до точек (2, 7/3) и (5, –1/2) также меньше 6,5

Но расстояние (–6, 5/2) равно 6.5.

Таким образом, точка (–6, 5/2) не лежит внутри круга.

10. Если расстояние между точками (4, p) и (1, 0) равно 5, то значение p i s

(A) 4 только

(В) ± 4

(C) — только 4

(Д) 0

Ответ: B

Пояснение: Согласно вопросу:

11. Площадь треугольника с вершинами A (3, 0), B (7, 0) и C (8, 4) составляет:

(А) 14

(В) 28

(К) 8

(Г) 6

Ответ: (C)

Пояснение: Площадь треугольника рассчитывается как,

Практические вопросы по тригонометрии для 10-го класса

(1) Докажите, что

Решение


(2) Докажите, что

(3) Если x sin ³ θ + y cos ³ θ = sin θ cos θ и x sin θ = y cos θ, то докажите, что x ² + y ² = 1.Решение

(4) Если a cos θ — b sin θ = c, то докажите, что (a sin θ + b cos θ) = ± √ (a ² + b ² — c ² ) Решение

(5) Птица сидит на вершине дерева высотой 80 м. С точки на земле угол подъема птицы составляет 45 °. Птица улетает горизонтально на такое расстояние, чтобы оставаться на постоянной высоте от земли. Через 2 секунды угол подъема птицы от той же точки составляет 30 °. Определите скорость, с которой летит птица.(√3 = 1,732) Решение

(6) Самолет летит параллельно поверхности Земли со скоростью 175 м / сек на высоте 600 м. Угол возвышения самолета от точки на поверхности Земли составляет 37 ° в данной точке. Через какой промежуток времени угол возвышения увеличивается до 53 °? (tan 53 ° = 1,3270, tan 37 ° = 0,7536) Решение

(7) Птица летит из точки A в сторону B под углом 35 °, в точке в 30 км от A. В точке B она меняет свой курс полета. и направляется в сторону C по азимуту 48 ° на расстоянии 32 км.

(i) Как далеко B к северу от A?

(ii) Как далеко B к западу от A?

(iii) Как далеко C находится к северу от B?

(iv) Как далеко C к востоку от B?

(sin 55 ° = 0,8192, cos 55 ° = 0,5736, sin 42 ° = 0,6691, cos 42 ° = 0,7431) Решение

(8) Два корабля плывут по морю по обе стороны от маяка. Углы падения двух кораблей, наблюдаемые с вершины маяка, составляют 60 ° и 45 ° соответственно.Если расстояние между кораблями составляет 200 [(√3 + 1) / √3] метров, найдите высоту маяка. Решение

(9) Здание и статуя находятся на противоположной стороне улицы друг от друга в 35 м друг от друга. С точки на крыше здания угол подъема вершины статуи составляет 24 °, а угол наклона основания статуи — 34 °. Найдите высоту статуи. (tan 24 ° = 0,4452, tan 34 ° = 0,6745) Решение

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.


Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM


Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямому и обратному изменению

Проблемы со словами по цене за единицу

Проблемы со словами по скорости за единицу

задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word задачи по сложным процентам

ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами

Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейным неравенством

Задачи

Проблемы со временем и рабочими словами

Проблемы со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами из теоремы Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами при сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями


Преобразование повторяющихся десятичных дробей в дроби

Десятичное представление рациональных чисел

с использованием длинного корня видение

Л.Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4


Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3


Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

.