Геометрия 10 класс задачи на готовых чертежах: Е.М.Рабинович Задачи на готовых чертежах 10-11

Содержание

Задачи на готовых чертежах 10 класс геометрия. | Материал для подготовки к ЕГЭ (ГИА) по геометрии (10 класс) на тему:

Слайд 1

РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Расстоянием между двумя не пересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым. Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью. Если ортогональная проекция на плоскость переводит прямую a в точку A ’ , а прямую b в прямую b ’ , то расстояние AB между прямыми a и b равно расстоянию A ’ B ’ от точки A ’ до прямой B ’ .

Слайд 2

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 B 1 . Ответ: 1 .

Слайд 3

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB и B 1 C 1 . Ответ: 1 .

Слайд 4

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB и C 1 D 1 . Ответ: 1 .

Слайд 5

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB и DE . Ответ: .

Слайд 6

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB и D 1 E 1 . Ответ: 2 .

Слайд 7

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CC 1 . Ответ: .

Слайд 8

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DD 1 . Ответ: 2 .

Слайд 9

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и B 1 C 1 . Ответ: . Решение: Продолжим стороны B 1 C 1 и A 1 F 1 до пересечения в точке G . Треугольник A 1 B 1 G равносторонний. Его высота A 1 H является искомым общим перпендикуляром. Его длина равна .

Слайд 10

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и C 1 D 1 . Ответ: .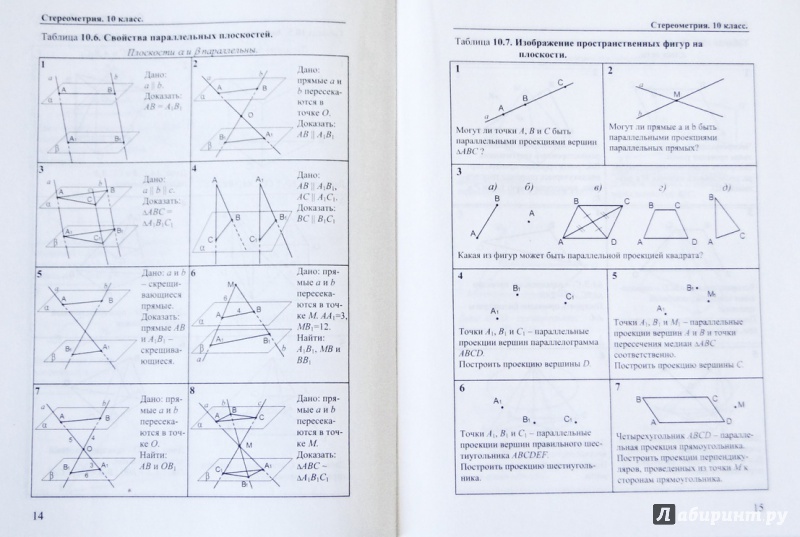 Решение: Искомым общим перпендикуляром является отрезок A 1 C 1 . Его длина равна .

Слайд 11

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1 . Ответ: . Решение: Искомым расстоянием является расстояние между параллельными плоскостями ADD 1 и BCC 1 . Оно равно .

Слайд 12

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CD 1 . Ответ: . Решение: Искомым общим перпендикуляром является отрезок AC . Его длина равна .

Слайд 13

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и DE 1 . Ответ: . Решение: Искомым общим перпендикуляром является отрезок A 1 E 1 . Его длина равна .

Слайд 14

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BD 1 . Решение: Искомым общим перпендикуляром является отрезок AB . Его длина равна 1 . Ответ: 1.

Слайд 15

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CE 1 . Ответ: . Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CEE 1 . Оно равно .

Слайд 16

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BE 1 . Ответ: . Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью BEE 1 . Оно равно .

Слайд 17

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CF 1 . Ответ: . Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CFF 1 . Оно равно .

Слайд 18

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между прямыми: AB 1 и DE 1 . Ответ: . Решение: Искомым расстоянием является расстояние между параллельными плоскостями ABB 1 и DEE 1 . Расстояние между ними равно .

Слайд 19

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между прямыми: AB 1 и CF 1 . Ответ: Решение: Искомым расстоянием является расстояние между прямой AB 1 и плоскостью CFF 1 . Оно равно .

Слайд 20

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BC 1 . Решение: Пусть O , O 1 –центры граней призмы. Плоскости AB 1 O 1 и BC 1 O параллельны. Плоскость ACC 1 A 1 перпендикулярна этим плоскостям. Искомое расстояние d равно расстоянию между прямыми AG 1 и GC 1 . В параллелограмме AGC 1 G 1 имеем AG = ; AG 1 = . Высота, проведенная к стороне AA 1 равна 1. Следовательно , d = . Ответ:

Слайд 21

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BD 1 . Решение: Рассмотрим плоскость A 1 B 1 HG , перпендикулярную BD 1 . Ортогональная проекция на эту плоскость переводит прямую BD 1 в точку H , а прямую AB 1 – в прямую GB 1 . Следовательно искомое расстояние d равно расстоянию от точки H до прямой GB 1 . В прямоугольном треугольнике GHB 1 имеем GH = 1; B 1 H = . Следовательно, d = . Ответ:

Слайд 22

В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB 1 и BE 1 .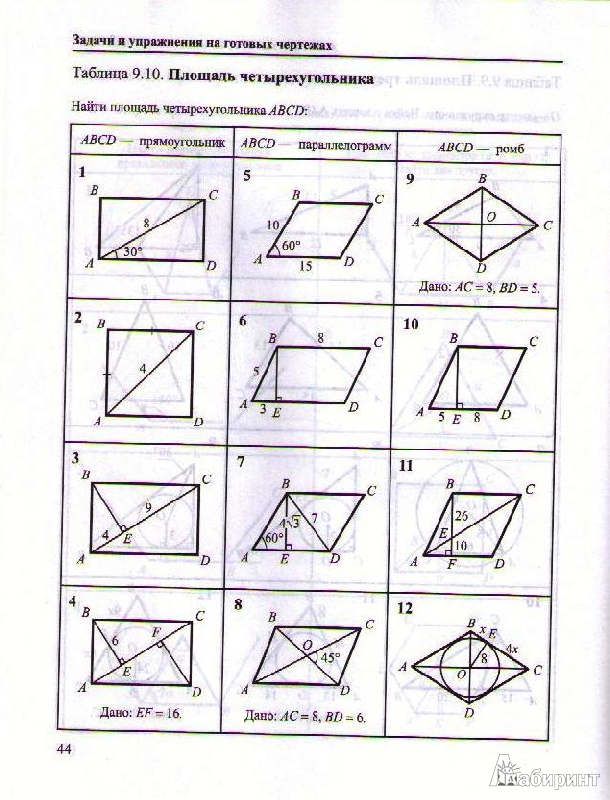 Решение: Рассмотрим плоскость A 1 BDE 1 , перпендикулярную AB 1 . Ортогональная проекция на эту плоскость переводит прямую AB 1 в точку G , а прямую BE 1 оставляет на месте . Следовательно искомое расстояние d равно расстоянию GH от точки G до прямой BE 1 . В прямоугольном треугольнике A 1 BE 1 имеем A 1 B = ; A 1 E 1 = . Следовательно, d = . Ответ:

Презентация «решение стереометрических задач по готовым чертежам».(хочу поделиться с коллегами)

Инфоурок › Геометрия ›Презентации›Презентация «решение стереометрических задач по готовым чертежам».(хочу поделиться с коллегами)

Скрыть

Выберите документ из архива для просмотра:

Выбранный для просмотра документ угол между прямыми.pptx

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Угол между двумя прямыми ГЕОМЕТРИЯ Задачи на готовых чертежах для подготовки к ЕГЭ 10 – 11 классы Антонова Г.

В.

2 слайд Описание слайда:

Антонова Г.В. ГЕОМЕТРИЯ Задачи на готовых чертежах для подготовки к ЕГЭ В презентации использована книга Э.Н.Балаян «Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10 – 11 классы»

3 слайд Описание слайда:

Антонова Г.В. Задача 1 Угол между двумя прямыми. Куб ABCD – квадрат ⇒ AC ⊥ BD Решение: A C B D

4 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 2 A C B D Решение:

5 слайд Описание слайда:

Антонова Г. В. Угол между двумя прямыми. Куб Задача 3 Решение: A C B D

6 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 4 Решение: A C B D

7 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 6 Решение: A C B D

8 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 7 Решение: A C B D

9 слайд Описание слайда:

Антонова Г. В. Угол между двумя прямыми. Куб Задача 8 Решение: A C B D

10 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 9 Решение: Решение аналогично решению задач № 7 – 8 A C B D

11 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 10 Решение: A C B D

12 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 11 Решение: A C B D

13 слайд Описание слайда:

Антонова Г. В. Угол между двумя прямыми. Куб Задача 12 Решение: A C B D

14 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 13 Решение: A C B D

15 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 14 Решение: Решение задачи аналогично решению задачи №5 презентации A C B D

16 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 15 Решение: AB∥DC ⇒ A C B D

17 слайд Описание слайда:

Антонова Г.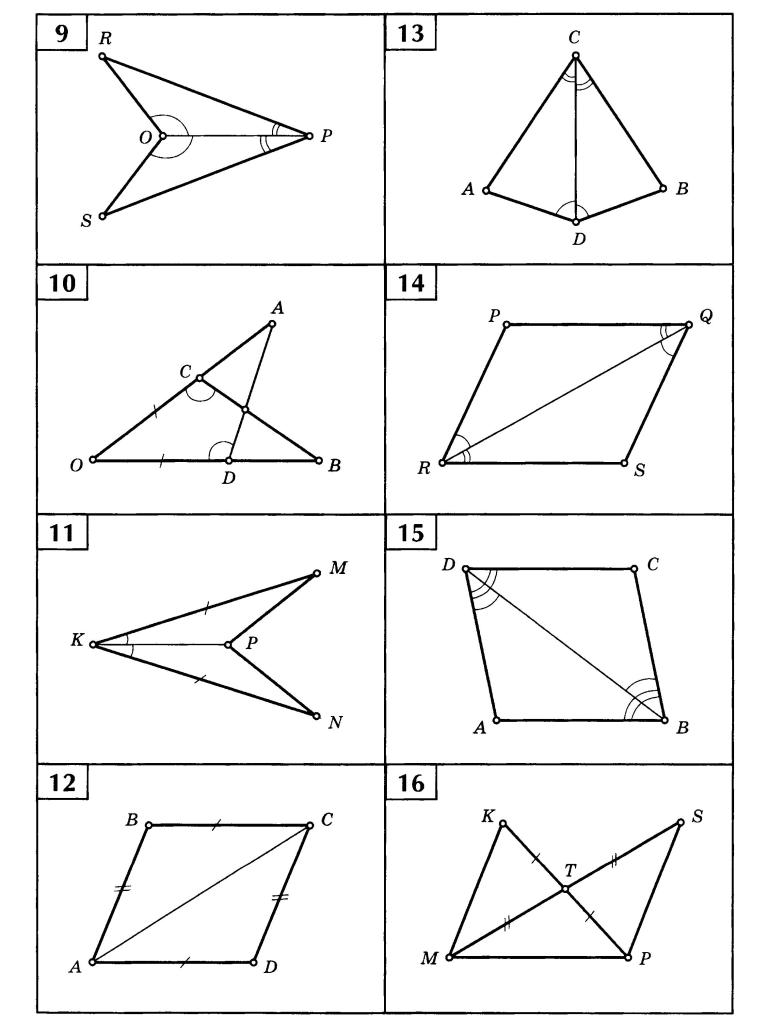 В. Угол между двумя прямыми. Куб Задача 16 Решение: A C B D

18 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 17 Решение: Решение задачи аналогично решению задачи №5 презентации A C B D

19 слайд Описание слайда:

Антонова Г.В. Угол между двумя прямыми. Куб Задача 18 Решение: A C B D

20 слайд Описание слайда:

1. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10 – 11 классы / Э.Н.Балаян. – Ростов н/Д: Феникс, 2013. – 217 с. : ил. – (Большая перемена). Антонова Г.В.

21 слайд Описание слайда:

http://www.

bg2001.ru/upload/iblock/616/4034-7.jpg http://lenagold.narod.ru/fon/clipart/s/svit/svitolk101.png http://megasklad.ru/data/photoes/s194064.jpg http://www.segment.ru/img_hits/4946015_1_small.jpg Интернет – ресурсы: Антонова Г.В.

22 слайд Описание слайда:

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Найдите материал к любому уроку,

указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-396593

Оставьте свой комментарий

Геометрия. 10-11 классы. Задания на готовых чертежах по стереометрии | Ковалева Г. | ISBN 9785705735594

Геометрия. 10-11 классы. Задания на готовых чертежах по стереометрии | Ковалева Г. | ISBN 9785705735594 | Купить книгу

Геометрия. 10-11 классы. Задания на готовых чертежах по стереометрии

Количество страниц

200

Нет в нашем ассортименте.

В пособии представлены задачи по стереометрии, предназначенные в первую очередь для организации устной работы учащихся, ориентированные для работы с учебником по геометрии Л.

С.Атанасяна и др., применимые к любому действующему учебнику. Каждая тема включает двенадцать задач, расположенных в порядке возрастания степени трудности и сопровождаемых готовыми чертежами. Учитель сможет выбрать те или иные задачи на готовых чертежах в зависимости от дидактической цели урока и уровня подготовленности учащихся, использовать чертеж в качестве опоры для восприятия, проведения анализа условий, открытия способов решения, поддерживать высокий темп работы школьников, предупреждать их типичные ошибки, успешно формировать предметные умения и метапредметные УУД в соответствии с ФГОС. Предназначено учителям математики, руководителям методических объединений. Похожие товары Информация о Brexit: огромные задержки с поставками в Великобританию.

Пожалуйста, рассчитывайте на двухнедельную задержку

Геометрия. Задачи на готовых чертежах для подготовки к ЕГЭ. 10-11 классы » LITMY.RU

Геометрия. Задачи на готовых чертежах для подготовки к ЕГЭ. 10-11 классы

Название: Геометрия. Задачи на готовых чертежах для подготовки к ЕГЭ. 10-11 классы
Автор: Балаян Э.Н.
Издательство: Феникс
Год: 2013
Страниц: 219
Формат: pdf
Размер: 27 mb
Качество: хорошее

Предлагаемая вниманию старшеклассников книга содержит более 600 разноуровневых задач по всем основным темам геометрии (стереометрии) 10-11 классов на готовых чертежах, скомпонованных в 80 таблицах. Эти задачи не только помогут учащимся углубить свои знания, проверить и закрепить практические навыки при систематическом изучении курса стереометрии, но и предоставляют хорошую возможность для самостоятельной эффективной подготовки к успешной сдаче ЕГЭ и вступительным экзаменам по математике.
Для удобства пользования книгой приводятся подробные решения к наиболее трудным задачам, а также краткие теоретические сведения, сопровождаемые определениями, рисунками и необходимыми справочными материалами. Ко всем задачам даны ответы. Пособие является прекрасным дополнением к существующим учебникам геометрии, предназначено учителям, старшеклассникам общеобразовательных школ, лицеев, колледжей как для подготовки к урокам, так и сдаче ЕГЭ, а также репетиторам.

Краткие теоретические сведения по курсу стереометрии X-XI классов.
Задачи в таблицах.
Угол между двумя прямыми.
Угол между прямой и плоскостью.
Угол между двумя плоскостями.
Расстояние от точки до плоскости.
Расстояние между двумя прямыми.
Площади сечений многогранников.
Площади поверхностей вращения плоских фигур.
Объемы тел вращения плоских фигур.
Объемы тел вращения многогранников.
Разные задачи.
Многогранники.
Фигуры вращения.
Решения наиболее трудных задач.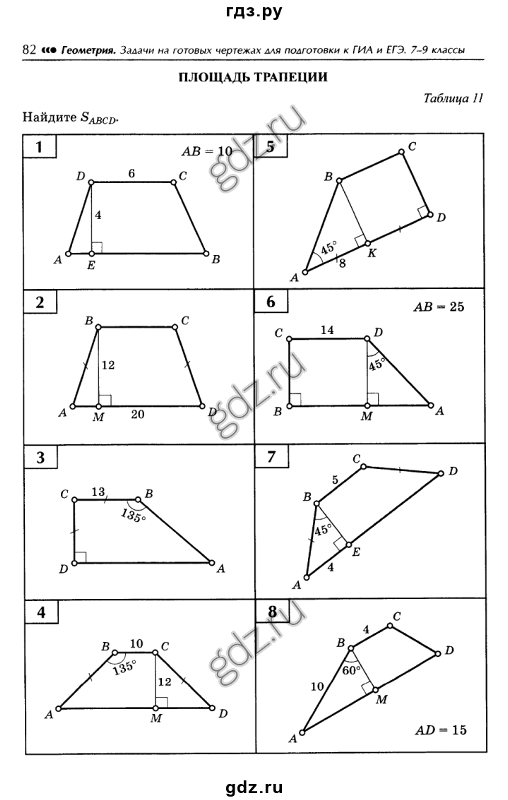

Скачать с облака

НЕ РАБОТАЕТTURBOBIT.NET? ЕСТЬ РЕШЕНИЕ, ЖМИ СЮДА!

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Геометрия

Геометрия — это всего около фигур и их свойств.

Если вам нравится играть с объектами или рисовать, то геометрия для вас!

Геометрию можно разделить на:

Плоская геометрия — это плоские формы, такие как линии, круги и треугольники … формы, которые можно нарисовать на листе бумаги

Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.

Подсказка: попробуйте нарисовать некоторые формы и углы по мере изучения … это помогает.

Точка, линия, плоскость и твердое тело

Точка не имеет размеров, только позиция
Линия одномерная
Самолет двумерный (2D)
Твердое тело трехмерное (3D)

Почему?

Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать мир вокруг нас.

Плоская геометрия

Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).

Полигоны

Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.

Вот еще несколько:

Круг

Теоремы о круге (расширенная тема)

Символы

В геометрии используется много специальных символов.Вот вам краткая справка:

Геометрические символы

Соответствующие и аналогичные

Уголки

Типы углов

Преобразования и симметрия

Преобразований:

Симметрия:

Координаты

Дополнительные разделы по геометрии плоскости

Пифагор

Конические секции

Теоремы о круге

Центры треугольника

Тригонометрия

Тригонометрия — отдельная тема, поэтому вы можете посетить:

Твердая геометрия

Solid Geometry — это геометрия трехмерного пространства, в котором мы живем. ..

… начнем с самых простых форм:

Общие 3D-формы

Многогранники и неполигранники

Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:

Многогранники (должны иметь плоские грани) :

Соединить точки: изометрический чертеж и закодированные планы — мероприятие

Введение / Мотивация

(Поднимите слайд-презентацию и покажите классу, начиная со слайда 3.) Пространственная визуализация полезна для практикующих инженеров, показала, что она является важным предиктором успеха студентов инженерных специальностей, а также является приобретенным навыком. Это означает, что мы можем улучшить наши навыки пространственной визуализации, практикуясь. Сегодня мы будем развивать навыки рисования трехмерных объектов. Навыки пространственной визуализации помогут вам во многих предметах и увлечениях, требующих воображения трехмерных фигур, таких как геометрия, химия, физика, легкая атлетика (например, теннис и гимнастика) и различные компьютерные игры. Практика пространственной визуализации позволяет вам легче понимать трехмерные фигуры и изображения и лучше справляться с этими предметами и хобби.

Часть 1: Изометрические чертежи

На этапе планирования любого инженерного проекта инженер должен уметь взять видение нового дизайна изнутри своей головы и проиллюстрировать его на листе бумаги или экране компьютера. Этот процесс — визуализация предмета как трехмерного объекта — включает в себя такие параметры, как глубина, ширина и высота.Без навыков пространственной визуализации инженеры не смогли бы представить новые идеи и передать их другим.

Изометрические виды удобны для отображения трехмерных объектов на двухмерном листе бумаги. В частности, мы используем бумагу с треугольными точками для изометрического рисования объектов. (Отобразите слайд 4, такой же, как на рисунке 1.) На этом изображении показан трехмерный куб, изображенный двумя разными способами. Слева куб нарисован неизометрически, так как углы в углах не равны, а стороны имеют разные площади. Однако справа куб нарисован так, что стороны куба соединяются в «углу», образуя равные углы в 120 °. Мы называем это изометрическим видом куба. Также обратите внимание, что на иллюстрации справа все стороны куба одинакового размера. Во время этого упражнения мы будем практиковаться в изометрическом рисовании фигур. (Слайд 5, такой же, как на рисунке 4, показывает изометрическое изображение дома с помощью AutoCAD.)

Рис. 1. Неизометрически нарисованный куб (слева) по сравнению с изометрически нарисованным кубом (справа).авторское право

Часть 2: Закодированные планы

Далее мы узнаем о закодированных планах. Прежде чем объяснять закодированные планы, давайте выполним упражнение, демонстрирующее важность использования закодированных планов. Во-первых, объединитесь с человеком рядом с вами.

(Предложите классу выполнить следующее упражнение: попросите партнера №1 закрыть глаза. Покажите всем учащимся-партнеру №2 левое изображение на слайде 6, такое же, как на рисунке 2.Сообщите партнеру №1, чтобы он держал глаза закрытыми, пока партнер №2 описывает изображение. Оставьте описание объекта на пару минут. Когда закончите, попросите партнера №1 нарисовать объект как можно точнее.)

Рис. 2. Изометрически нарисованный объект (слева) и его закодированный план (справа). Copyright

Для такого простого на вид объекта это было довольно сложно, правда? Возможно, вы описали объект такими фразами:

Состоит из шести кубиков.
Три куба сложены один поверх другого. Рядом два куба, также поставленные один поверх другого. Рядом с этой стопкой находится один единственный куб.

Даже с таким объяснением возможно, что ваш партнер неправильно представил объект. Представьте, что если бы вы были инженером, которому нужно было спроектировать гораздо более сложный объект, чем тот, который вы пытались описать, это было бы еще сложнее! Именно поэтому мы используем закодированные планы в технических чертежах. Закодированные планы — это инструмент, используемый инженерами для отображения трехмерных объектов на двухмерных поверхностях. Кодированный план определяет форму конструкции или объекта, состоящего из блоков. (Щелкните, чтобы открыть правую часть слайда 6, которая такая же, как правая часть рисунка 2 — закодированный план того же изображения, только что описанный и нарисованный учащимися.) Например, здесь показан закодированный план. Обратите внимание, что углы объекта помечены буквами. Также обратите внимание, что числа внутри квадратов представляют количество кубиков, уложенных друг на друга.Далее мы выполним некоторые упражнения, чтобы попрактиковаться в создании закодированных планов и изометрических чертежей.

Как исправить проблемы с неоднородной геометрией в 3D-моделях

Тип немножечной ошибки № 1: Многосвязная геометрия

Форма на изображении ниже представляет собой типичную немножечную геометрию, которую также можно найти как « Т-образный ». В этом случае есть три грани, разделяющие одну кромку.

Исправить такие проблемы, не связанные с многообразием, просто: вы должны устранить поверхность, не относящуюся к коллектору, либо придав ей объем, либо полностью удалив ее.

Тип неоднородной ошибки № 2: несколько поверхностей, соединенных одной вершиной

На следующем рисунке мы видим другую распространенную немногообразную геометрию, которую часто называют «дугообразной». В этом случае к вершине подключено более двух поверхностей. Это практически невозможно, так как не может быть нескольких граней, имеющих общую вершину, но не может быть ребра.

Эту ошибку можно устранить, отключив кубики друг от друга или полностью удалив один из них.

Тип необратной ошибки № 3: Открытые объекты

Эта модель представляет собой куб с поверхностями с нулевым объемом, а также с двумя отсутствующими поверхностями. В реальном мире такая модель существовать не может.

Чтобы исправить эту геометрию, у вас есть две альтернативы. Либо отрегулировать толщину стенок коробки, либо закрыть коробку, добавив две новые поверхности. В обоих случаях куб имеет допустимый объем и его можно напечатать на 3D-принтере.

Тип немножечной ошибки № 4: Внутренние грани

На следующем изображении мы видим каркас куба.С этой точки зрения мы видим совершенно ненужное внутреннее лицо.

Эту ошибку легко исправить, просто удалив внутреннюю грань. Если вы не удалите это лицо, программное обеспечение 3D-принтера не сможет прочитать ваш файл.

Тип неоднородной ошибки № 5: Противоположные нормали

В этом примере мы видим одну форму с двумя смежными гранями, которые имеют противоположные нормали. Эту ошибку трудно обнаружить, поскольку она наименее очевидна.

Как только вы обнаружите ошибку, ее легко исправить, просто перевернув нормали, чтобы они указывали в одном направлении.

% PDF-1.4 % 00001 0 объект > 1> 2> 3> 4> 5> 6> 7> 8> 9> 10> 11> 12> 13> 14> 15> 16> 17> 18> 19> 20> 21> 22> 23> 24> 25 > 26> 27> 28> 29> 30> 31> 32> 33> 34> 35> 36> 37> 38> 39> 40> 41> 42> 43> 44> 45> 46> 47> 48> 49> 50 > 51> 52> 53> 54> 55> 56> 57> 58> 59> 60> 61> 62> 63> 64> 65> 66> 67> 68> 69> 70> 71> 72> 73> 74> 75 > 76> 77> 78> 79> 80> 81> 82> 83> 84> 85> 86> 87> 88> 89> 90> 91> 92> 93> 94> 95> 96> 97> 98> 99> 100 > 101> 102> 103> 104> 105> 106> 107> 108> 109> 110> 111> 112> 113> 114> 115> 116> 117> 118> 119> 120> 121> 122> 123> 124> 125 > 126> 127> 128> 129> 130> 131> 132> 133> 134> 135> 136> 137> 138> 139> 140> 141> 142> 143> 144> 145> 146> 147> 148> 149> 150 > 151> 152> 153> 154> 155> 156> 157> 158> 159> 160> 161> 162> 163> 164> 165> 166> 167> 168> 169> 170> 171> 172> 173> 174> 175 > 176> 177> 178> 179> 180> 181> 182> 183> 184> 18 5> 186> 187> 188> 189> 190> 191> 192> 193> 194> 195> 196> 197> 198> 199> 200> 201> 202> 203> 204> 205> 206> 207> 208> 209> 210> 211> 212> 213> 214> 215> 216> 217> 218> 219> 220> 221> 222> 223> 224> 225> 226> 227> 228> 229> 230> 231> 232> 233> 234> 235> 236> 237> 238> 239> 240> 241> 242> 243> 244> 245> 246> 247> 248> 249> 250> 251> 252> 253> 254> 255> 256> 257> 258> 259> 260> 261> 262> 263> 264> 265> 266> 267> 268> 269> 270> 271> 272> 273> 274> 275> 276> 277> 278> 279> 280> 281> 282> 283> 284> 285> 286> 287> 288> 289> 290> 291> 292> 293> 294> 295> 296> 297> 298> 299> 300> 301> 302> 303> 304> 305> 306> 307> 308> 309> 310> 311> 312> 313> 314> 315> 316> 317> 318> 319> 320> 321> 322> 323> 324> 325> 326> 327> 328> 329> 330> 331> 332> 333> 334> 335> 336> 337> 338> 339> 340> 341> 342> 343> 344> 345> 346> 347> 348> 349> 350> 351> 352> 353> 354> 355> 356> 357> 358> 359> 360> 361> 362> 363> 364> 365> 366> 367> 368> 369> 370> 371> 372> 373> 374> 375> 376> 377> 378> 379> 380> 381> 382> 383> 384> 385> 386> 387> 388> 389> 390> 391> 392> 393> 394> 395> 396> 397> 398> 399> 400> 401> 402> 403> 404> 405> 406> 407> 408> 409> 410> 411> 412> 413> 414> 415> 416> 417> 418> 419> 420> 421> 422> 423> 424> 425> 426> 427> 428> 429> 430> 431> 432> 433> 434> 435> 436> 437> 438> 439> 440> 441> 442> 443> 444> 445> 446> 447> 448> 449> 450> 451> 452> 453> 454> 455> 456> 457> 458> 459> 460> 461> 462> 463> 464> 465> 466> 467> 468> 469> 470> 471> 472> 473> 474> 475> 476> 477> 478> 479> 480> 481> 482> 483> 484> 485> 486> 487> 488> 489> 490> 491> 492> 493> 494> 495> 496> 497> 498> 499> 500> 501> ] >>>> endobj 00002 0 объект > endobj 00003 0 объект > endobj 00004 0 объект > / ProcSet [/ PDF / ImageB / ImageC] >> / MediaBox [0 0 463.5 765] / CropBox [0 0 463,5 765] / Содержание 5 0 R >> endobj 00005 0 объект > поток x + 2133U0

Перейти к задачам по геометрии Страница 1, 1-50, Школа, Колледж, Онлайн-обучение, Электронное обучение

	Задачи по геометрии Go Страница 1

	Проблемы открытой геометрии Проблемы Десять задач геометрии Визуальный указатель Параллельные линии Перпендикулярные линии Коллинеарные точки Треугольник Метрические отношения Четырехугольник Треугольник и квадраты Полигоны Пентагоны Шестиугольники Семиугольники Восьмиугольники Круг Треугольник Центры Конгруэнтность Сходство, соотношения, пропорции
	Геометрия Проблема 1492. Прямой треугольник, высота, центры, угол, измерение.
	Геометрия Задача 1491. Циклический четырехугольник, диагональ, вписанная окружность, угол, измерение.
	Геометрия Задача 1490. Треугольник, Цвиан, вписанная окружность, касательная, Измерение.
	Геометрия Проблема 1489. Прямой треугольник, биссектриса угла, перпендикуляр, измерение.
	Геометрия Задача 1488. Прямой треугольник, высота, вписанная окружность, касательная, измерение.
	Геометрия Задача 1487. Прямой треугольник, высота, вписанная окружность, касательная, измерение.
	Геометрия Задача 1486. Прямой треугольник, высота, вписанная окружность, касательная, измерение.
	Геометрия Задача 1485. Треугольник, Ортоцентр, Высота, Круг, Диаметр, Касательная, Измерение.
	Геометрия Проблема 1484. Прямой треугольник, высота, окружности, внутренний радиус, измерение.
	Геометрия Задача 1483. Равнобедренный прямоугольный треугольник, эксцентр, перпендикуляр, измерение.
	Геометрия Задача 1482. Прямой треугольник, перпендикуляр, двойной угол, измерение.
	Динамическая геометрия 1481. Пять касательных или описанных четырехугольников, теорема Пито, конгруэнтность, пошаговая иллюстрация. GeoGebra, iPad.
	Динамическая геометрия 1480. Японская теорема для циклического многоугольника, Сангаку, триангуляция, непересекающиеся диагонали, сумма Inradii, инвариант, пошаговая иллюстрация.GeoGebra, iPad.
	Динамическая геометрия 1479. Треугольник, окружность, биссектриса угла, Серединный перпендикуляр, хорда, конциклические точки, параллельные линии, пошаговая иллюстрация. GeoGebra, iPad.
	Динамическая геометрия 1478. Циклочевиан, теорема Ройшле-Теркема, параллельные Чевианы, треугольник, окружность, секущая линия, пошаговая иллюстрация.GeoGebra, iPad.
	Динамическая геометрия 1477. Теорема Микеля о пентаграмме, пятиугольник, треугольник, окружности, конциклические точки, пошаговая иллюстрация. GeoGebra, iPad.
	Dynamic Geometry 1476. Теорема Дроза-Фарни о прямой, треугольник, ортоцентр, перпендикуляр, коллинеарные средние точки, пошаговая иллюстрация.GeoGebra, iPad.
	Динамическая геометрия 1475. Теорема Клиффорда о пересекающихся окружностях, Пошаговая иллюстрация, GeoGebra, iPad.
	Динамическая геометрия 1473. Теорема Косницы, треугольник, четыре центра окружности, параллельная линия, пошаговая иллюстрация.
	Dynamic Geometry 1472. Циклический четырехугольник, перпендикулярные диагонали, прямоугольник, пошаговая иллюстрация.
	Динамическая геометрия 1471. Равносторонний треугольник, внутренняя / внешняя точка, центры начала, точки касания, параллельные линии, пошаговая иллюстрация.
	Dynamic Geometry 1470. Тангенциальный четырехугольник, вписанная окружность, касательная, Параллель, Ромб, Пошаговая иллюстрация.
	Динамическая геометрия 1469. Треугольник, окружной радиус, внутренний радиус, средние точки, дуги, сумма расстояний, пошаговая иллюстрация.
	Динамическая геометрия 1468. Теорема Штейнера, треугольник, окружной радиус, внутренний радиус, сумма эксрадиусов, пошаговая иллюстрация.
	Задача геометрии 1467. Квадрат, прямоугольник, треугольник, площадь.
	Проблема геометрии 1466. Тангенциальный четырехугольник, линия Ньютона, центр, середина, диагональ, коллинеарные точки. Пошаговая иллюстрация с использованием GeoGebra.
	Задача геометрии 1465. Тангенциальный четырехугольник, центр, вписанная окружность, равная сумма площадей. Пошаговая иллюстрация с использованием GeoGebra.
	Задача геометрии 1464. Четырехугольник, внутренняя точка, середина сторон, равная сумма площадей. Пошаговая иллюстрация с использованием GeoGebra.
	Задача геометрии 1463. Параллелограмм, внутренняя точка, противоположные треугольники с одинаковой суммой площадей. Пошаговая иллюстрация с использованием GeoGebra.
	Проблема геометрии 1462. Линия Ньютона, линия Ньютона-Гаусса, полный четырехугольник, середины сторон и диагоналей, Коллинеарные точки.
	Задача геометрии 1461. Четырехугольник, треугольник, углы, 30-60 градусов, конгруэнтность, вспомогательные линии.
	Динамическая геометрия 1460. Линия Ньютона-Гаусса, полный четырехугольник, середины диагоналей, Коллинеарные точки, пошаговая иллюстрация с использованием GeoGebra.
	Геометрия Задача 1459. Два треугольника, ортоцентр, середина, перпендикуляр, пошаговое изображение. Иллюстрация с использованием GeoGebra.
	Геометрия Проблема 1458. Треугольник, Incircles, Excircle, Area, Пошаговая иллюстрация с использованием GeoGebra.
	Геометрия Задача 1457. Высоты, Круги, Сходство, Произведение длин Inradii, iPad. Пошаговая иллюстрация с использованием GeoGebra.
	Геометрия Проблема 1456. Высота, Ортический треугольник, Окружность, Параллельные линии, Сходство, Площадь, iPad. Пошаговая иллюстрация с использованием GeoGebra.
	Геометрия Задача 1455. Точка Нагеля, Excircles, Incircle, конгруэнтные сегменты, iPad. Пошаговая иллюстрация с использованием GeoGebra.
	Геометрия Проблема 1454. Пересекающиеся окружности, перпендикулярные линии, циклический четырехугольник, коллинеарность Точки, iPad. Пошаговая иллюстрация с использованием GeoGebra.
	Геометрия Задача 1453. Два полукруга, циклический четырехугольник, конциклические точки, iPad.
	Динамическая геометрия 1452. Японская теорема, Сангаку, Циклический четырехугольник, центр, прямоугольник, внутренний радиус. Шаг за шагом иллюстрация с использованием GeoGebra.
	Динамическая геометрия 1451. Ортополь прямой. Шаг за шагом иллюстрация с использованием GeoGebra.
	Динамическая геометрия 1450. Ортолин, линия Штейнера, полный четырехугольник, коллинеальные ортоцентры. Шаг за шагом иллюстрация с использованием GeoGebra.
	Задача геометрии 1400. Треугольник с тремя прямоугольниками по бокам, биссектрисы, параллелизм.
	Задача геометрии 1391. Два треугольника, соотношение площадей, окружность.
	Задача геометрии 1381. Параллелограмм, внешняя точка, треугольник, площадь.
	Задача геометрии 1371: Equilic Четырехсторонний 5
	Задача геометрии 1361. Треугольник, два круга с девятью точками, круг Фейербаха, круг Эйлера, конгруэнтные углы, эскиз, приложения для iPad.
	Задача геометрии 1200 Квадрат, прямоугольный треугольник, перпендикуляр, 90 градусов, равные площади.
	Проблема геометрии 900 Пересекающиеся окружности, общий внешний касательный, секущий, угол, конгруэнтность. GeoGebra, Анимация HTML5 для планшетов. Решение.
	Проблема геометрии 800 Теорема де Гуа, теорема Пифагора в трехмерном пространстве, тетраэдр, кубическая вершина, треугольная пирамида, вершина, высота, площадь прямоугольного треугольника, площадь основания, площадь проекции. Решение.
	Проблема геометрии 700. Равносторонний треугольник, круг, круговой сегмент, середина стороны, метрические соотношения. Решение.
	Проблема геометрии 600 Круг, площадь, касательная, полукруг, точка касания. Решение.
	Задача геометрии 500. Окружность, диаметр, хорда, перпендикуляр, мера. Решение.
	Задача геометрии 400. Треугольник, биссектриса угла, окружность, перпендикуляр, конгруэнтность. Решение.
	Задача геометрии 300. Касательные к окружности, секущие, квадрат. Решение.
	Задача геометрии 200. Прямой треугольник, вписанная окружность, округлости, точки Касание, Inradius. Решение.
	Задача геометрии 100. Круг Площадь, Книга лемм Архимеда. Решение.
	Проблема геометрии 1. Треугольник, медиана, углы, 45 градусов. Решение
Перейти на страницу: Предыдущая \| 1 \| 2 \| 3 \| 4 \| 5 \| 6 \| 7 \| 8 \| 9 \| 10 \| 11 \| 12 \| 13 \| 14 \| 15 \| Следующий

CBSE Class 10 Mathematics Coordinate Geometry MCQs Set D, Multiple Choice questions for Coordinate Geometry

CBSE Class 10 Mathematics Coordinate Geometry MCQs Set D.Вопросы с несколькими вариантами ответов стали неотъемлемой частью экзаменационной системы CBSE. Практически во всех экзаменах есть раздел для MCQ. Студентам рекомендуется обращаться к прилагаемой базе данных MCQ и регулярно практиковаться. Это поможет им определить свои слабые стороны и поможет им лучше набрать баллы на экзамене. Родители должны загрузить и отдать MCQ своим детям для практики.

1. Точка A (–5, 6) находится на расстоянии:

(a) 61 единица от исходной точки (b) 11 единиц от исходной точки

2.Если точки (1, x), (5, 2) и (9, 5) лежат на одной прямой, то значение x равно

(a) 5/2 (b) -5/2 (c) –1 ( г) 1

3. Конечными точками диаметра окружности являются (2, 4) и (–3, –1). Радиус окружности us

4. Отношение, в котором ось x делит отрезок прямой, соединяющий точки (5, 4) и (2, –3), составляет:

(a) 5: 2 (b) 3: 4 (c) 2: 5 (d) 4: 3

5. Точка, которая разделяет отрезок прямой, соединяющий точки (7, –6) и (3, 4) в соотношении 1: 2 внутренне лежит в

(a) I квадрант (b) II квадрант (c) III квадрант (d) IV квадрант

6.Точка, которая лежит на серединном перпендикуляре отрезка прямой, соединяющего точки A (–2, — 5) и B (2, 5), равна:

(a) (0, 0) (b) (0, 2 ) (c) (2, 0) (d) (–2, 0)

7. Четвертая вершина D параллелограмма ABCD, три вершины которого — это A (-2, 3), B (6, 7) и C (8,3) равно:

(a) (0, 1) (b) (0, -1) (c) (-1, 0) (d) (1, 0)

8. Если точка P (2, 1) лежит на отрезке прямой, соединяющем точки A (4, 2) и B (8, 4), то

9.Три вершины параллелограмма, взятые по порядку: (- 1, — 6), (2, — 5) и (7, 2). Четвертая вершина —

(a) (1, 4) (b) (1, 1) (c) (4, 4) (d) (4, 1)

10. Если A и B точки (- 3, 4) и (2,1) соответственно, то координаты точек на AB, созданных так, что AC = 2BC, равны

(a) (2, 4) (b) (3, 7) ( c) (7, –2) (d) ни один из этих

11. Расстояние точки (4, a) от оси x составляет половину расстояния от оси y, тогда a =

(a) 2 (б) 8 (в) 4 (г) 6

12.Треугольник образован точками 0 (0, 0), A (5,0) и B (0,5). Число точек, имеющих целые координаты (как x, так и y) и строго внутри треугольника, равно

(a) 10 (b) 17 (c) 16 (d) 6

13. Если P (l, 2) , Q (4,6), R (5,7) и S (a, b) — вершины параллелограмма PQRS, тогда

(a) a = 2, b = 4 (b) a = 3, b = 4 (c) a = 2, b = 3 (d) a = 3, b = 5

14. Количество точек на оси x, которые находятся на расстоянии 2 единиц от (2, 4) равно

(а) 2 (б) 1 (в) 3 (г) 0

15.Расстояние точки (h, k) от оси x равно

(a) h (b) k (c) | h | (г) | k |

16. Вершины треугольника — это (0, 0), (3, 0) и (0, 4). Его ортоцентр находится в точке

(а) (0, 3) (б) (4, 0) (в) (0, 0) (г) (3, 4)

17. Площадь треугольник с вершинами в точках (a, b + c), (b, c + a) и (c, a + b) равен

(a) a + b + c (b) a + b — c (c) a — b + c (d) 0

18.