10 класс ответы на вопросы
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
ГДЗ 10 класс Ответы на вопросы геометрия 10‐11 класс Атанасян, Бутузов
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
ГДЗ за 10‐11 класс по Геометрии Атанасян Л. С., Бутузов В.Ф.
С., Бутузов В.Ф.
gdz-bot.ru
НайтиНавигация по гдз
1 класс Русский язык Математика Английский язык Окружающий мир Литература Информатика Музыка Человек и мир 2 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка Технология Человек и мир 3 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика МузыкаGRE Количественное сравнение Геометрические практические задачи
Вот набор из 7 практических вопросов по контролю качества. Пояснения будут в конце статьи.
Пояснения будут в конце статьи.
Примечание: все вопросы количественного сравнения имеют одинаковые четыре варианта ответа. Я не копировал варианты ответов для каждого вопроса в этом сообщении, поэтому обратите внимание на варианты ответов ниже:
а. Количество А больше.
г. Количество B больше.
г. Эти две величины равны.
г. Связь не может быть определена из предоставленной информации.
1) На схеме AC = 6. CE = 12, DF = 4, а AB параллельна DE.
2)
3) На диаграмме JL = 4 и JK = 6.
4) На схеме О — центр окружности, а АВ — диаметр.Область J — это область между хордой AC и дугой окружности.
5) На схеме треугольник MNP равносторонний.
6) На схеме JKLM представляет собой квадрат. Точка S — это середина KL, а точка T — центр квадрата. Точка O находится на сегменте ST и является центром окружности, проходящей через K и L.
Точка O находится на сегменте ST и является центром окружности, проходящей через K и L.
7)
Геометрия на GRE QC
Как вы понимаете, нет гарантии, что любая геометрическая диаграмма на всем участке GRE Quant нарисована в масштабе.Фактически, большинство появляющихся диаграмм специально разработано, чтобы обмануть вас самым жестоким обманчивым способом, который только можно представить. Например, если GRE дает
без дальнейших объяснений или уточнений, наивный и доверчивый участник теста GRE подумает: «Хорошо, равносторонний треугольник», тогда как на самом деле это может быть любое из этих значений:
Никогда не обманывайтесь, веря диаграмме. В частности, одна большая группа вопросов GRE QC Geometry дает вам диаграммы, которые выглядят определенным образом, но оставляют некоторую двусмысленность открытой, и ваша задача — выявить двусмысленность, различные геометрические возможности, и не поддаваться влиянию веры в вводящие в заблуждение диаграмма.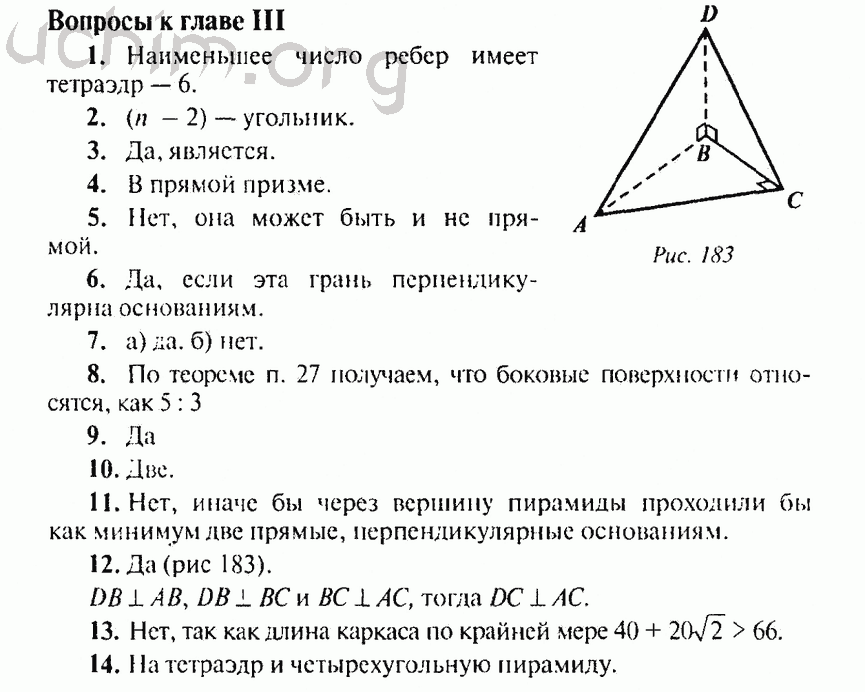 Некоторые из вышеперечисленных вопросов относятся к этому типу.
Некоторые из вышеперечисленных вопросов относятся к этому типу.
Еще одна партия вопросов GRE QC Geometry, конкретизирующих все в деталях, и ваша задача — выполнить какой-либо расчет длины, угла или площади и сравнить их с чем-то.
По крайней мере, при рассмотрении вопроса о геометрии GRE QC важно понимать, является ли это типом неоднозначной диаграммы или типом «все указанное». Первый случай имеет высокую вероятность получения ответа (D) !
Сводка
Если предыдущее обсуждение дало вам некоторое представление о вопросе, вы можете вернуться и взглянуть на него еще раз.Пожалуйста, дайте нам знать о своем опыте работы с вопросами GRE Geometry в разделах комментариев ниже.
Практическое объяснение проблем
1) Треугольники CBA и CDE подобны, поэтому все соответствующие длины пропорциональны. Каждая длина в CBA равна 1/2 соответствующей длины в CDE. Подумайте о DF, высоте в CDE и длине, которой она будет соответствовать в CBA: высоте от вершины B до основания AC.
Позвоните по телефону h .Поскольку DF = 4, h = 2.
Теперь для CBA у нас есть высота h = 2 и основание AC = 6.
Ответ = (В)
2) Здесь все исправлено и уточнено. Треугольник ABC — это прямоугольный треугольник, потому что самая длинная сторона — это диаметр. Подробнее читайте в этом сообщении в блоге о GMAT. В прямоугольном треугольнике ABC AB = 4 — гипотенуза. Обратите внимание, это НЕ треугольник 3-4-5, потому что гипотенуза равна 4.
Мы можем извлечь квадратный корень, чтобы найти длину AC, но нам это не нужно.AC — это сторона квадрата, поэтому AC в квадрате — это площадь квадрата. Площадь 7.
Ответ = (C)
3) Это обманчивая диаграмма. Угол в L кажется прямым, но абсолютно ничто на диаграмме или в тексте не гарантирует, что это прямой угол. Треугольник может быть:
Слева треугольник «раздавлен» почти до плоскости, и его можно раздавить еще больше, почти до нуля. Конечно, площадь может быть меньше 11. Напротив, если JK и JL перпендикулярны, тогда площадь будет A = 0,5bh = (0,5) (4) (6) = 12, что больше 11. В зависимости от диаграмма, это может пойти в любом направлении.
Конечно, площадь может быть меньше 11. Напротив, если JK и JL перпендикулярны, тогда площадь будет A = 0,5bh = (0,5) (4) (6) = 12, что больше 11. В зависимости от диаграмма, это может пойти в любом направлении.
Ответ = (D)
4) Мы знаем, что AB — это диаметр, и мы знаем, что угол ACB равен 90 °. Все это мы знаем. Мы не знаем положение точки C. На приведенной диаграмме точка C расположена так, что две области выглядят примерно одинаково. Перемещая точку C, мы могли радикально изменить ситуацию.Например, мы могли бы переместить C в сторону B, сделав область J намного больше.
Или мы могли бы переместить точку C на другую сторону, ближе к точке A, и в этом случае треугольник будет намного больше, а Область J намного меньше.
Поскольку мы можем варьировать точку C для получения различных соотношений, мы не можем дать фиксированный ответ.
Ответ = (D)
5) Это сложная задача, но мы можем решить ее полностью, не прикасаясь к калькулятору.
Первый шаг — провести высоту от каждой вершины равностороннего треугольника до середины противоположной стороны. Это разделит равносторонний треугольник на шесть равных треугольников 30-60-90. Подробнее об этих треугольниках читайте в этом блоге GMAT. Очень удобно помнить, что таким образом можно разделить любой равносторонний треугольник.
Обратите внимание, что OP, OM и ON — это радиусы окружности. Скажем для удобства, что r = 2, поэтому OPO = OM = ON = 2.Посмотрите на вершину треугольника 30-60-90. Гипотенуза OP = 2, поэтому сторона, противоположная углу 30 °, составляет половину этого угла, OT = 1. Длина оставшейся стороны, противоположной 60 °, должна быть:
Площадь треугольника TOP будет:
Шесть из этих треугольников составляют весь равносторонний треугольник, так что это
Это площадь всего равностороннего треугольника. Между тем, круг имеет радиус r = 2, поэтому
Теперь заштрихованная область — это площадь круга за вычетом площади равностороннего элемента, поэтому площадь заштрихованной области составляет:
Теперь у нас есть номера по областям обоих регионов:
Независимо от того, что квадратный корень из 3 равен, он явно меньше 2, поэтому величина A меньше 2, а величина B немного больше 2.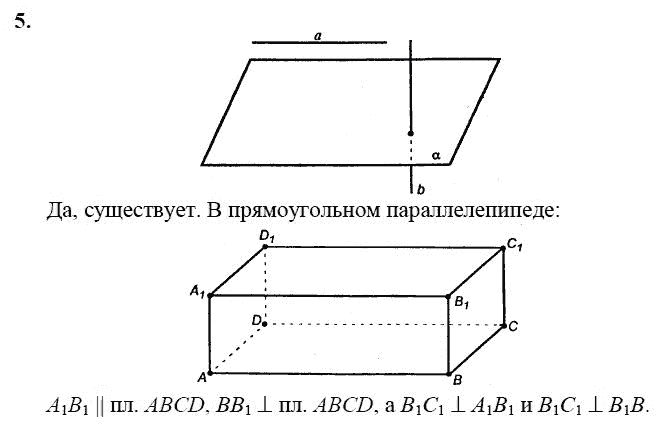
Ответ = (В)
6) Обратите внимание, что единственное, что не исправлено в задаче, — это положение точки O на отрезке ST. Это может быть верх или низ этого сегмента. Подумайте о последствиях.
Если мы переместим точку O к вершине круга, так что она будет очень близко к S, то мы получим относительно маленькие круги.
В пределе, в котором O находилась в точке S, круг был бы таким, диаметр которого равнялся бы стороне квадрата: такой круг мог бы полностью поместиться внутри квадрата, просто касаясь каждой стороны в его средней точке.Очевидно, такой круг будет иметь гораздо меньшую площадь, чем квадрат.
С другой стороны, мы могли бы переместить точку O вниз к точке T, центру квадрата. В результате получаются относительно большие круги.
В пределе, в котором O находилась в точке T, круг аккуратно содержал бы квадрат, проходящий через четыре угла. Такой круг явно имеет большую площадь, чем квадрат.
Поскольку мы можем выбрать позицию для точки O, которая допускает связь в любом случае, мы не можем определить окончательную связь между количествами.
Ответ = (D)
7) Сложный вопрос. Давайте подойдем к этому так. Иногда очень полезно ввести переменную в геометрическую задачу. Я собираюсь сказать, что AC = x и BC = 1. Обратите внимание, что AB = x + 1. Тогда
Что будет, если x = 3? Обратите внимание:
Ясно, что они не равны, как должно быть. Что будет, если мы увеличим x? Что ж, тогда AC / BC = x просто становится больше, но AB / BC становится меньше, поэтому они не будут приближаться к равенству.Фактически, они будут отдаляться друг от друга.
Что произойдет, если x станет меньше? Что ж, тогда AC / BC = x явно становится меньше, а дробь 1 / x становится больше, когда ее знаменатель становится меньше, поэтому AB / BC будет больше. В этом случае они будут двигаться навстречу друг другу: больший становится меньше, а меньший — больше. Это означает, что они могут стать равными, если мы переместим x в этом направлении, меньше 3. Другими словами, x должен быть меньше 3.
Здесь этого достаточно, чтобы определить, что ответ на вопрос QC — (B) .
Дополнительная информация для любознательных:
Если вам интересно, обратите внимание, что если x = 2, то:
Они ближе, но не равны. Если x = 1, то
Вот, они прострелили друг друга. Теперь маленький слишком большой, а большой слишком маленький! Мы промахнулись. Это говорит нам, что правильное значение x находится в диапазоне от 1 до 2.
Фактически, некоторые студенты могут понять, что приведенная выше диаграмма и уравнение являются определением золотого сечения, и на самом деле это правильное значение x.
Если вы были знакомы с золотым сечением, это было бы сокращением для этой конкретной проблемы, но в целом вам не нужно ничего знать о золотом сечении для GRE. Золотое сечение играет большую роль в сакральной геометрии и во всех видах эзотерической мудрости (египетские храмы, Парфенон, картины Леонардо, готические соборы и т. Д.), Так что вы можете найти его интересным, но все это выходит далеко за рамки всего, имеющего отношение к успехов на GRE !! 🙂
Д.), Так что вы можете найти его интересным, но все это выходит далеко за рамки всего, имеющего отношение к успехов на GRE !! 🙂
Если хотите еще больше попрактиковаться в математике GRE, ознакомьтесь с нашими математическими вопросами GRE с ответами и пояснениями!
стр.S. Готовы улучшить свой GRE? Начни сегодня.
Самые популярные ресурсы
РешенияNCERT для класса 10 по математике, глава 7, координатная геометрия
Решения NCERT для класса 10 по математике, глава 7
| , класс: | 10 |
| Subject: | Maths — गणित |
| Координатная геометрия |
10-я математика Глава 7 Решения
Решения NCERT для класса 10 Математика глава 7 упражнения по координатной геометрии из 7.1–7,4 приведены ниже для бесплатной загрузки. Все содержание обновлено для академической сессии 2020-21. Автономные приложения, основанные на этих решениях, также предназначены для новой сессии. Присоединяйтесь к дискуссионному форуму, чтобы обсудить свои сомнения и ответить на вопросы, которые задают ваши друзья.
Присоединяйтесь к дискуссионному форуму, чтобы обсудить свои сомнения и ответить на вопросы, которые задают ваши друзья.
10-я глава 7 по математике Упражнение 7.1
10-я глава 7 по математике Упражнение 7.2
10-я математическая глава 7 Упражнение 7,3
- 4
Математика класса 10 Глава 7 Упражнение 7.1 Решения на видео
Математика класса 10 Упражнение 7.1 Решение с пояснением Математика класса 10 Решение упражнения 7.2 на видео Математика класса 10 Глава 7 Решения упражнения 7. 2 в Видео
2 в Видео
Математика для класса 10. Упражнение 7.2. Решение с пояснением. . Класс 10. Математическое упражнение. 7.2. Решение на видео..
. Математика. Глава 7. Упражнение. 7.3. Решения……Решение 3 с объяснением Математическое упражнение для класса 10 7.3 Решение в видео Математическое решение для класса 10 Глава 7 Упражнение 7.4 Решения в видео
youtube.com/embed/pan4TMrx12E?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/> Математическое упражнение для класса 10 7.4 Решение с объяснением Математическое упражнение для класса 10 Решение в видео Решения NCERT для математики класса 10 Глава 7
Каковы цели координатной геометрии в математике класса 10?
Цели координатной геометрии
Чтобы найти расстояние между двумя разными точками, координаты которых заданы, и найти координаты точки, которая внутренне делит отрезок линии, соединяющий две точки в заданном соотношении.Чтобы найти координаты средней точки соединения двух точек, чтобы получить координаты центроида треугольника с заданными вершинами.
Дать важные результаты в координатной геометрии?
Важные результаты в координатной геометрии
Координаты начала координат равны (0, 0)
Координата y каждой точки на оси x равна 0, а координата x каждой точки на оси y- ось равна 0.
Две оси XOX ‘и YOY’ делят плоскость на четыре части, называемые квадрантами.
Вопросы за предыдущие годы
ВОПРОСЫ ОДНОЙ МАРКИ
1. Если расстояние между точками (4, k) и (1, 0) равно 5, то каковы возможные значения k? [CBSE 2017]
ТРИ ЗНАКА ВОПРОСЫ
1. Площадь треугольника составляет 5 квадратных единиц. Две его вершины — это (2, 1) и (3, -2). Если третья вершина — (7/2, y), найдите значение y. [CBSE 2017]
2. Покажите, что треугольник ABC, где A (-2, 0), B (2, 0), C (0, 2), и треугольник PQR, где (-4, 0), Q (4, 0) ), R (0, 4) — аналогичные треугольники.2), (0, 0) не будут коллинеарны. [CBSE 2017]
Знать о координатной геометрии
В координатной геометрии мы изучаем, что расстояние от точки до оси Y называется ее координатой x или абсциссой (абсцисса — это латинское слово, которое означает отсечение ), а расстояние от точки до оси x называется ее координатой y или ординатой (ордината — это латинское слово, означающее «поддерживать порядок»). Абсцисса и ордината вместе образуют координату точки в декартовой системе.Координаты точки на оси x имеют вид (x, 0), а точки на оси y имеют форму (0, y). Чтобы узнать больше о координатной геометрии, пройдите по образцам задач NCERT для класса 10 по математике.
Абсцисса и ордината вместе образуют координату точки в декартовой системе.Координаты точки на оси x имеют вид (x, 0), а точки на оси y имеют форму (0, y). Чтобы узнать больше о координатной геометрии, пройдите по образцам задач NCERT для класса 10 по математике.
Исторические факты!
Рене Декарт (1596–1650) был французским философом, математиком, чья работа «Геометрия» включает его применение алгебры к геометрии, из которой мы теперь имеем декартову геометрию.
Важные вопросы по математике 10 класса Глава 7
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं (2, 3), (- 1, 0), (2, -4).
त्रिभुज के शीर्ष A (2, 3), B (-1, 0) और C (2, -4) हैं।
त्रिभुज के क्षेत्रफल व्यंजक
= 1/2 [x_1 (y_2 — y_3) + x_2 (y_3 — y_1) + x_3 (y_1 — y_2)] द्वारा त्रिभुज ABC का क्षेत्रफल
= 1/2 [2 {0 — (- 4)} + (-1) {(-4) — 3} + 2 (3-0)]
= 1/2 [8 + 7 + 6]
= 21/2
= 10,5 वर्ग मात्रक
Найдите значение ‘k’, для которого точки (7, -2), (5, 1) и (3, k) коллинеарны.
A (7, -2), B (5, 1), C (3, k)
Площадь треугольника, образованного тремя коллинеарными точками, равна нулю.2 + 9y — 3y — 27 = 0
⇒ y (y + 9) — 3 (y + 9) = 0
⇒ (y + 9) (y — 3) = 0
⇒ (y + 9) = 0 या (y — 3) = 0
⇒ y = — 9 या y = 3
Примечания к редакции по математике Глава 7 — Координатная геометрия (10-й класс)
Декартова система координат
В декартовой системе координат существует декартова плоскость, состоящая из двух числовых линий, перпендикулярных друг другу, т.е.е. ось x (горизонтальная) и ось y (вертикальная) , которая представляет две переменные. Эти две перпендикулярные линии называются координатной осью.
Эти две перпендикулярные линии называются координатной осью.
Точка пересечения этих двух линий называется центром или началом координатной плоскости. Его координаты (0, 0).
Любая точка на этой координатной плоскости представлена упорядоченной парой чисел.Пусть (a, b) — упорядоченная пара, тогда a — координата x, а b — координата y.
Расстояние до любой точки от оси y называется ее координатой x или абсциссой , а расстояние до любой точки от оси x называется ее координатой y или ординатой .
Декартова плоскость разделена на четыре квадранта I, II, III и IV.
Уравнение прямой
Уравнение линии используется для построения графика линии на декартовой плоскости.
Уравнение прямой записывается в форме пересечения наклона как
y = mx + b
, где m — наклон линии, а b — точка пересечения с y.
Чтобы сначала найти наклон прямой, нам нужно преобразовать уравнение в форму пересечения наклона, тогда мы сможем легко получить наклон и точку пересечения по оси y.
Формула расстояния
Расстояние между любыми двумя точками A (x 1 , y 1 ) и B (x 2 , y 2 ) рассчитывается по
Пример
Найдите расстояние между точками D и E на данном рисунке.
Решение
Это показывает, что совпадает с теоремой Пифагора . Как в теореме Пифагора
Расстояние от исходной точки
Если нам нужно найти расстояние до любой точки от начала координат, то одна точка — это P (x, y), а другая точка — это сама начало координат, то есть O (0,0). Таким образом, согласно приведенной выше формуле расстояния, это будет
.
Формула раздела
Если P (x, y) — любая точка на отрезке AB, который делит AB в соотношении m: n, то координаты точки P (x, y) будут
. Формула средней точки
Если P (x, y) — средняя точка отрезка AB, который делит AB в соотношении 1: 1, то координаты точки P (x, y) будут
. Площадь треугольника
Здесь ABC — треугольник с вершинами A (x 1 , y 1 ), B (x 2 , y 2 ) и C (x 3 , y 3 ).Чтобы найти площадь треугольника, нам нужно провести перпендикуляры AP, BQ и CR от A, B и C, соответственно, к оси x. Теперь мы видим, что ABQP, APRC и BQRC — все трапеции.
Площадь треугольника ABC = Площадь трапеции ABQP + Площадь трапеции APRC — Площадь трапеции BQRC.
Следовательно,
Замечание : Если площадь треугольника равна нулю, то данные три точки должны быть коллинеарны.
Пример
Давайте посмотрим, как найти площадь четырехугольника ABCD, вершинами которого являются A (-4, -2), B (-3, -5), C (3, -2) и D (2, 3).
Если ABCD — четырехугольник, мы получаем два треугольника, соединяя A и C. Чтобы найти площадь четырехугольника ABCD, мы можем найти площадь ∆ ABC и ∆ ADC, а затем сложить их.
Площадь многоугольника
Подобно треугольнику, мы можем легко найти площадь любого многоугольника, если мы знаем координаты всех вершин многоугольника.
Если у нас есть многоугольник с числом вершин n, то формула для площади будет
Где x 1 — координата x вершины 1, а y n — координата y n-й вершины и т. Д.
Пример
Найдите площадь данного четырехугольника.
Решение
Найти площадь данного четырехугольника —
Площадь четырехугольника 45,5, так как площадь всегда положительна.
Центроид треугольника
Центроид треугольника — это точка, в которой все три медианы треугольника пересекаются друг с другом.
Здесь ABC — треугольник с вершинами A (x 1 , y 1 ), B (x 2 , y 2 ) и C (x 3 , y 3 ). Центроид треугольника — это точка с координатами (x, y).
Координаты центроида будут рассчитаны как
Примечания
В координатной геометрии многоугольники образованы координатами x и y его вершин. Итак, чтобы доказать, что данная цифра:
No. Фигуры из четырех точек Доказать 1. Квадрат Его четыре стороны равны, и диагонали также равны. 2.
Ромб Его четыре стороны равны. 3. Ромб, но не квадрат Четыре стороны равны и диагонали не равны. 4. Прямоугольник Его противоположные стороны равны, диагонали равны. 5. Параллелограмм Его противоположные стороны равны. 6. Параллелограмм, но не прямоугольник Его противоположные стороны равны, но диагонали не равны.
No. Фигуры из трех точек Доказать 1. Разносторонний треугольник Если ни одна из его сторон не равна. 2. Равнобедренный треугольник
Для 9–10 классов учеников, занимающихся геометрией. Используйте кликер для ответов на вопросы.
Используйте кликер для ответов на вопросы.
Презентация на тему: «Для учащихся 9-10 классов, занимающихся геометрией. Используйте кликер для ответов на вопросы.»- стенограмма презентации:
1
Для учащихся 9-10 классов, занимающихся геометрией. Используйте кликер, чтобы отвечать на вопросы.
2
Q1: Что это за теорема? Если три стороны одного треугольника конгруэнтны трем сторонам другого треугольника, то треугольники конгруэнтны A.Конгруэнтность бокового угла-стороны (SAS) B. Конгруэнтность угла-стороны-угла (ASA) C. Конгруэнтность стороны-стороны-стороны (SSS) D. Конгруэнтность угла-угла-стороны (AAS)
3
Q2: Что это за теорема? Если две стороны и прилегающий угол одного треугольника совпадают с соответствующими частями другого треугольника, треугольники конгруэнтны. A. Конгруэнтность угол-угол-сторона (AAS) B. Сопоставление сторон-угла-стороны (SAS) C. Сопоставление стороны-стороны-стороны (SSS) D.Угол-боковой-угол (ASA) Конгруэнтность
A. Конгруэнтность угол-угол-сторона (AAS) B. Сопоставление сторон-угла-стороны (SAS) C. Сопоставление стороны-стороны-стороны (SSS) D.Угол-боковой-угол (ASA) Конгруэнтность
4
Q3: Что это за теорема? Если два угла и включенная сторона одного треугольника совпадают с соответствующими частями другого треугольника, треугольники конгруэнтны. A. Конгруэнтность «угол-сторона-угол» (ASA) B. Сопоставление «сторона-угол-сторона» (SAS) C. Сопоставление «сторона-сторона-сторона» (SSS) D. Конгруэнция «угол-угол-сторона» (AAS)
5
Q4: Что это за теорема? Если два угла и не включенная сторона одного треугольника конгруэнтны соответствующим частям другого треугольника, треугольники конгруэнтны.A. Сопоставление сторон-сторон-сторон (SSS) B. Сопоставление сторон-угла-сторон (SAS) C. Сопоставление угла-стороны-угла (ASA) D. Сопоставление угла-угла-стороны (AAS)
.
Чтобы найти расстояние между двумя разными точками, координаты которых заданы, и найти координаты точки, которая внутренне делит отрезок линии, соединяющий две точки в заданном соотношении.Чтобы найти координаты средней точки соединения двух точек, чтобы получить координаты центроида треугольника с заданными вершинами.
Координаты начала координат равны (0, 0)
Координата y каждой точки на оси x равна 0, а координата x каждой точки на оси y- ось равна 0.

Две оси XOX ‘и YOY’ делят плоскость на четыре части, называемые квадрантами.
1. Если расстояние между точками (4, k) и (1, 0) равно 5, то каковы возможные значения k? [CBSE 2017]
ТРИ ЗНАКА ВОПРОСЫ
1. Площадь треугольника составляет 5 квадратных единиц. Две его вершины — это (2, 1) и (3, -2). Если третья вершина — (7/2, y), найдите значение y. [CBSE 2017]
2. Покажите, что треугольник ABC, где A (-2, 0), B (2, 0), C (0, 2), и треугольник PQR, где (-4, 0), Q (4, 0) ), R (0, 4) — аналогичные треугольники.2), (0, 0) не будут коллинеарны. [CBSE 2017]
 Абсцисса и ордината вместе образуют координату точки в декартовой системе.Координаты точки на оси x имеют вид (x, 0), а точки на оси y имеют форму (0, y). Чтобы узнать больше о координатной геометрии, пройдите по образцам задач NCERT для класса 10 по математике.
Абсцисса и ордината вместе образуют координату точки в декартовой системе.Координаты точки на оси x имеют вид (x, 0), а точки на оси y имеют форму (0, y). Чтобы узнать больше о координатной геометрии, пройдите по образцам задач NCERT для класса 10 по математике.= 1/2 [2 {0 — (- 4)} + (-1) {(-4) — 3} + 2 (3-0)]
= 1/2 [8 + 7 + 6]
= 21/2
= 10,5 वर्ग मात्रक

Площадь треугольника, образованного тремя коллинеарными точками, равна нулю.2 + 9y — 3y — 27 = 0
⇒ y (y + 9) — 3 (y + 9) = 0
⇒ (y + 9) (y — 3) = 0
⇒ (y + 9) = 0 या (y — 3) = 0
⇒ y = — 9 या y = 3
Декартова система координат
В декартовой системе координат существует декартова плоскость, состоящая из двух числовых линий, перпендикулярных друг другу, т.е.е. ось x (горизонтальная) и ось y (вертикальная) , которая представляет две переменные.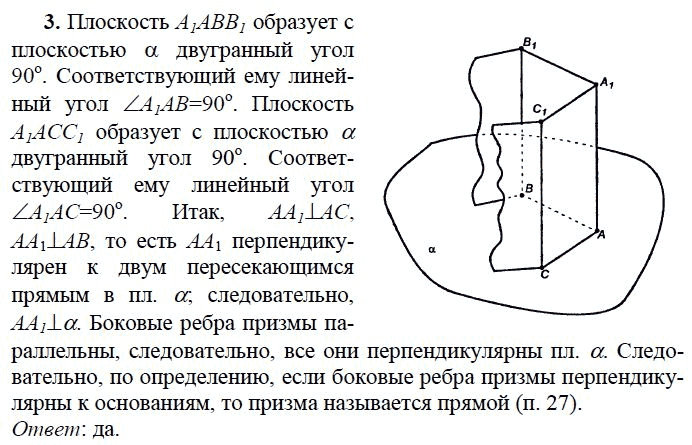 Эти две перпендикулярные линии называются координатной осью.
Эти две перпендикулярные линии называются координатной осью.
Точка пересечения этих двух линий называется центром или началом координатной плоскости. Его координаты (0, 0).
Любая точка на этой координатной плоскости представлена упорядоченной парой чисел.Пусть (a, b) — упорядоченная пара, тогда a — координата x, а b — координата y.
Расстояние до любой точки от оси y называется ее координатой x или абсциссой , а расстояние до любой точки от оси x называется ее координатой y или ординатой .
Декартова плоскость разделена на четыре квадранта I, II, III и IV.

-reshenie-zadacha-11.jpg)


 Используйте кликер для ответов на вопросы.
Используйте кликер для ответов на вопросы.  A. Конгруэнтность угол-угол-сторона (AAS) B. Сопоставление сторон-угла-стороны (SAS) C. Сопоставление стороны-стороны-стороны (SSS) D.Угол-боковой-угол (ASA) Конгруэнтность
A. Конгруэнтность угол-угол-сторона (AAS) B. Сопоставление сторон-угла-стороны (SAS) C. Сопоставление стороны-стороны-стороны (SSS) D.Угол-боковой-угол (ASA) Конгруэнтность

 С., Бутузов В.Ф.
С., Бутузов В.Ф. 2 в Видео
2 в Видео 
