4 кл матем ответы: ГДЗ Математика 4 класс учебник 2 часть. Моро, Бантова, Волкова. Готовые ответы на задания, решебник

Олимпиадные задания по математике с ответами, 4 класс

Олимпиадные задания для школьников по математике.

4 класс

В тестовых задачах возможен один вариант правильного ответа.

ЧАСТЬ 1

Задача 1.

Два брата учатся в одной школе: Вова – во втором классе, Петя – в седьмом. Второклассник утверждает, что в школе больше учеников младших классов, семиклассник – что больше школьников. Кто прав?

А) Вова Б) Петя В) Оба правы Г) Оба не правы

Верный ответ: Б) Петя Пояснение: Все ученики младших классов – школьники. Кроме того, есть ещё ученики средних и старших классов. Значит прав Петя, т.к. школьников больше.

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

Задача 2.

Ребята стоят в ряд. Аня третья слева и шестая справа. Сколько детей стоит в ряду?

А) 6 Б) 8 В) 10 Г) 12

Верный ответ: Б) 8 Пояснение:1 2 3/6 5 4 3 2 1

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

Задача 3. ( 1 балл)

Отец в 3 раза старше сына. Вместе им 40 лет. Сколько лет отцу?

А) 20 лет Б) 30 лет В) 40 лет Г) 50 лет

Верный ответ: Б) 30 лет

1) Возраст отца = возраст сына • 3, значит, 40 лет = возраст сына + возраст сына • 3 = возраст сына • 4. 40 : 4 = 10 лет –возраст сына. 10 • 3 = 30 – возраст отца.

2) Возраст сына – 1 часть, отца – 3 части. 1 + 3 = 4 ч., 4 ч. = 40 лет, 1 ч. = 10 лет сыну, 10 • 3 = 30 лет отцу.

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

Задача 4. ( 1 балл)

Коле 39 месяцев. Сколько ему лет?

А) 2 года Б) 3 года В) 4 года Г) 5 лет

Верный ответ: Б) 3 года

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

Задача 5 ( 1 балл)

Саша пишет за минуту одну строчку, а Ваня – 3. За сколько минут они напишут вместе 48 строк?

А) 10 минут Б) 11 минут В)12 минут Г) 13 минут

Верный ответ: В)12 минут

1) 3 + 1 = 4 строки напишут за 1 мин вдвоем,

2) 48 : 4 = 12 мин – за столько напишут вместе

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

Задача 6. ( 1 балл)

Только на одной из этих пяти картинок площадь закрашенной части не равна площади белой части. На какой?

Верный ответ: Д)

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

Задача 7. ( 1 балл)

Что не равно семи? 

(А) число дней в неделе (Б) полдюжины (Д) число цветов радуги
(Б) число букв в слове МОЛОДЕЦ (Г) частное чисел 4900 и 700

Верный ответ: Б)

Количество баллов: 1 балл

Критерии: 1 балл за верный ответ, 0 баллов — во всех других случаях.

ЧАСТЬ 2

Задача 1.

Отца зовут Николай Васильевич Марков, мать – Елена Евгеньевна Маркова. Дочь назвали в честь маминого папы. Напиши фамилию, имя и отчество девочки.

Верный ответ: Евгения Николаевна Маркова

Количество баллов: 2 балла

Критерии: 1 балл за верно написанное имя и отчество, 2 балла – за верно написанное имя, отчество, фамилия.

Задача 2.

Двадцатого марта Роме исполнилось 4 года 4 месяца и 4 дня. Какого числа у Ромы день рождения?

Верный ответ: 16 ноября.

Количество баллов: 2 балла

Критерии: 1 балл – записан верный ответ; 2 балла – записан верный ответ, даны пояснения.

Задача 3.

Составь самое большое трёхзначное число, состоящее из разных нечётных цифр и цифры 0. Каким оно будет, чётным или нечётным?

Верный ответ: 970, чётное.

Самые большие нечётные цифры – 9 и 7. Цифра 0 самая маленькая. Самая большая цифра должна означать сотни, следующая десятки, самая маленькая единицы

Количество баллов: 2 балла

Критерии: 1 балл – записан верный ответ; 2 балла – записан верный ответ, даны пояснения.

Задача 4.

Яна и Вика учатся в четвёртом классе, а Инна в третьем. Яна и Инна ходят в кружок пения, а Вика в кружок танцев. Кто ходит в кружок пения и учится в четвёртом классе?

Верный ответ: Яна

Количество баллов: 2 балла

Критерии: 1 балл – записан верный ответ; 2 балла – записан верный ответ, даны пояснения.

Задача 5.

Один будильник спешит на 25 минут и показывает 7 часов 50 минут. Какое время показывает другой будильник, который отстает на 15 минут?

Верный ответ: 7 часов 10 минут

Количество баллов: 2 балла

Критерии: 1 балл – записан верный ответ; 2 балла – записан верный ответ, даны пояснения.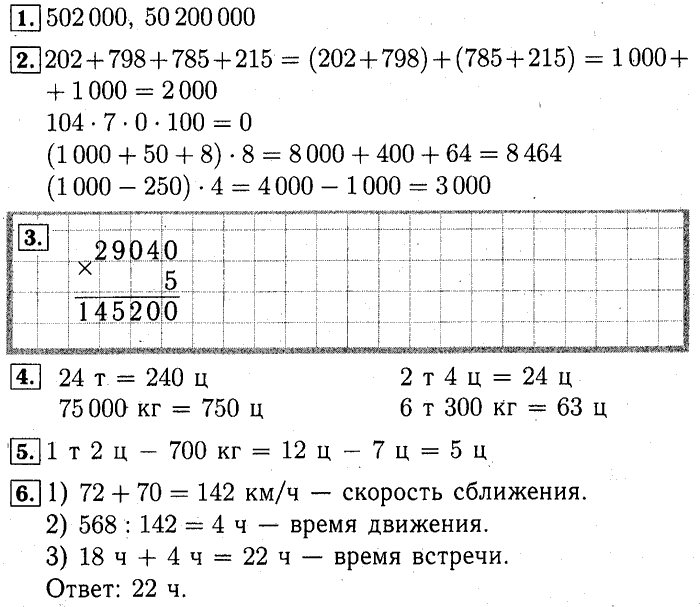

ЧАСТЬ 3

Задача 1.

В каждой тройке расположение чисел подчинено определённой закономерности. Найди общее правило для всех троек чисел.

А) 4 32 3 Б) 5 40 11 В) 9 72 43

Верный ответ: • 8 – 29 Например: 4 (• 8 =) 32 (– 29 =) 3

Количество баллов: 3 балла

Критерии: 2 балла – за верный ответ, 3 балла – обоснование ответа, 0 баллов во всех других случаях.

Задача 2.

Плитки двух видов были выложены на стене в шахматном порядке. Несколько плиток упали со стены (см. рисунок). Сколько полосатых плиток упало?

Верный ответ: 7 полосатых плиток

Количество баллов: 3 балла

Критерии: 2 балла – за верный ответ, 3 балла – обоснование ответа, 0 баллов во всех других случаях.

Задача 3.

Если Дима даст Кате 10 кубиков, у них будет кубиков поровну. На сколько кубиков у Димы больше, чему Кати?

Верный ответ: У Димы на 20 кубиков больше.

Предположим, Дима отдал Кате 10 кубиков, и у них стало кубиков поровну,а потом забрал их обратно. У Димы стало на 10 кубиков больше, чем было при равенстве, а у Кати на 10 кубиков меньше, чем было при равенстве. Значит, разница между Диминой и Катиной суммой кубиков увеличилась на 20 кубиков. У Димы на 20 кубиков больше.

Количество баллов: 3 балла

Критерии: 2 балла – за верный ответ, 3 балла – обоснование ответа, 0 баллов во всех других случаях.

Задача 4.

5 рабочих за 4 секунды забили 5 гвоздей. Сколько гвоздей забьют 7 рабочих за 12 секунд?

Верный ответ: 21 гвоздь.

5 рабочих забили 5 гвоздей, значит, каждый рабочий забил по 1 гвоздю. На это ушло 4 сек. Значит, за 12 сек. один рабочий забьёт 3 гвоздя. 7 рабочих за это же время забьют 21 гвоздь.

Количество баллов: 3 балла

Критерии: 2 балла – за верный ответ, 3 балла – обоснование ответа, 0 баллов во всех других случаях.

Задача 5.

У Светы в 3 раза больше карандашей, чем у Васи. Если Света отдаст Васе 2 карандаша, у них станет карандашей поровну. Сколько карандашей у Светы и сколько у Васи?

Верный ответ: У Светы 6 карандашей, а у Васи 2 карандаша.

Все карандаши можно разделить на 4 равные части – 3 части у Светы и 1 часть у Васи. Чтобы разделить карандаши поровну, у каждого должно быть по 2 части. Значит, Света должна отдать Васе 1 часть карандашей. Получается, что 2 карандаша – это 1 часть всех карандашей. Значит, у Светы 6 карандашей, а у Васи 2 карандаша.

Количество баллов: 3 балла

Критерии: 2 балла – за верный ответ, 3 балла – обоснование ответа, 0 баллов во всех других случаях.

Страница 73 (учебник Моро 2 часть 4 класс) ответы по математике

284. Выполни деление с объяснением.
2820 : 235, 7222 : 314, 14484 : 426, 25916 : 418.

Нужно разделить 2820 на 235.
Чтобы легче было найти цифру частного, разделим 282 на 200.
Для этого разделим 2 на 2, в частном получим 1.
Это пробная цифра, её нужно проверить.
Умножим 235 на 1, получится 235.
Вычтем 235 из 282, получим 47.
Добавим к нему оставшиеся 0 единиц — 470.
Находим вторую цифру частного: 470 : 235 = 2 (единицы). Частное — 12.

Нужно разделить 7222 на 314.
Чтобы легче было найти цифру частного, разделим 722 на 300.
Для этого разделим 7 на 3, в частном получим 2.
Это пробная цифра, её нужно проверить.
Умножим 314 на 2, получится 628.
Вычтем 628 из 722, получим 94.
Добавим к нему оставшиеся 2 единицы — 942.
Находим вторую цифру частного: 942 : 314 = 3 (единицы). Частное — 23.

Нужно разделить 14484 на 426.
Чтобы легче было найти цифру частного, разделим 1448 на 400.
Для этого разделим 14 на 4, в частном получим 3.
Это пробная цифра, её нужно проверить.
Умножим 426 на 3, получится 1278.
Вычтем 1278 из 1448, получим 170.
Добавим к нему оставшиеся 4 единицы — 1704.
Находим вторую цифру частного: 1704 : 426 = 4 (единицы). Частное — 34.

Нужно разделить 25916 на 418.
Чтобы легче было найти цифру частного, разделим 2591 на 400.
Для этого разделим 25 на 4, в частном получим 6.
Это пробная цифра, её нужно проверить.
Умножим 418 на 6, получится 2508.
Вычтем 2508 из 2591, получим 83.
Добавим к нему оставшиеся 6 единиц — 836.
Находим вторую цифру частного: 836 : 418 = 2 (единицы). Частное — 62.

285.

260 * 403 — (568 * 5 — 1840) = 260 * 403 — (2840 — 1840) = 260 * 403 — 1000 = 104780 — 1000 = 103780

671 * 223 + (6000 — 87 * 40) = 671 * 223 + (6000 — 3480) = 671 * 223 + 2520 = 149633 + 2520 = 152153

286. При ремонте дома нужно покрасить 150 рам. Один маляр может это сделать за 15 дней, а другой — за 10 дней. За сколько дней маляры смогут выполнить задание, работая вместе?

1) 150 : 15 = 10 рам в день красит первый маляр.
2) 150 : 10 = 15 рам в день красит второй маляр.
3) 15 + 10 = 25 рам в день красят оба маляра.
4) За 150 : 25 = 6 дней они выполнят задание.
Ответ: за 6 дней.

287. Туристы совершили восхождение на гору. В первый день они поднялись на 750 м. Во второй день они осилили две третьих высоты, взятой вчера. B третий день они поднялись на высоту, составляющую половину той, которая была достигнута в первые два дня. На какую высоту туристы поднялись за эти три дня?

1) 750 * 2 : 3 = 500 м — поднялись туристы во второй день.
2) 750 + 500 = 1250 м — поднялись туристы за первые два дня.
3) 1250 : 2 = 625 м — поднялись туристы в третий день.
4) 1250 + 625 = 1875 м — поднялись туристы за три дня.
Ответ: 1875 м.

288. Объясни, что показывает каждое выражение, составленное по данным таблицы.

1) 260 : 4 — скорость первого объекта.
2) 240 : 4 — скорость второго объекта.
3) 260 + 240 — начальное расстояние между объектами.
4) 260 — 240 — на сколько километров первый объект прошёл больше, чем второй.
5) (260 + 240) : 4 — скорость сближения объектов.
6) (260 — 240) : 4 — на сколько скорость первого объекта больше скорость второго.

289. Мама моложе бабушки на 24 года. На сколько лет мама будет моложе бабушки через 4 года? через 10 лет?

Разница возрастов не зависит от количества прошедших лет.
Ответ: на 24 года.

Задание под знаком вопроса.

8640 : 27 = 320

507 * 372 + (9200 — 800 : 4) = 507 * 372 + (9200 — 200) = 507 * 372 + 9000 = 188604 + 9000 = 179604

Задание на полях.
Цепочка.

8000 → 200 → 2 → 180 → 18 → 72

Математика ответы 4 класс

ОЛИМПИАДА – 2016    по математике

4 класс                           (школьный тур)  

1. За верное решение — 4 б., полный ответ — 1 б.

    Минус 0,5 б. за неверное или отсутствие наименования.

    Итого: 5 б.
    Решение.

    4+7+12=23 (п.) отдали на уху.
    (32-23):3=3 (п.) осталось у каждого.
     3+4=7 (п.) у Ниф-Нифа.
     3+7=10 (п.) у Наф-Нафа.
     3+12=15 (п.) у Нуф-Нуфа.

2. За каждую цепочку по 1 б. Итого: 5 б.
    3
    21
    6
    18
    50

3. За верный ответ 1 б.
    1023

4. За верное решение. 2 б.

5. Верно — 2 б.
    1) Коля. 2) Петя. 3) Ваня. 4) Сеня.

6. За верное решение — 2 б.

7. Правильный ответ — 3 б.
    Ответ: 10100

    ИТОГО  20 баллов.

 

№ задания	1	2	3	4	5	6	7
Балл	5	5	1	2	2	2	3	20

 

 

Олимпиадные задания

ans-engl-4-5-prigl-msk-21-22

  1264   15. 09.2021

Содержание Part 1 — Listening (time – 15 minutes , 15 points) Task 1 Task 2 Part 2 — Reading (time-15 minutes, 7 points) Part 3  — Use of English (time – 30 minutes, 33 points) Task 1 Task 2 Task 3 Критерии оценивания Part 1 — Listening (time – 15 minutes , 15 points) […]

  6301   21.12.2020

Содержание Задача 6.1 Задача 6.2 Задача 6.3 Задача 6.4 Задача 6.5 Задача 6.6 Задача 6.7 Задача 6.8 Задача 6.1 Найдите любое решение ребуса где A, B, C — три различные ненулевые цифры; запись AB означает двузначное число, составленное из цифр A и B; запись CCC означает трёхзначное число, состоящее только из цифр C. В качестве […]

  10334   30.11.2020

Содержание Задача 5.1 Задача 5.2 Задача 5.3 Задача 5.4 Задача 5.5 Задача 5.6 Задача 5.7 Задача 5.8 Задача 5.1. Денис расставил числа от 1 до 9 в клетки квадрата 3 × 3 так, что сумма чисел во всех строках и во всех столбцах равна 15. А Лёша стёр числа от 1 до 5 и вместо […]

  12076   24.11.2020

Содержание Задача 4.1 Задача 4.2 Задача 4.3 Задача 4.4 Задача 4.5 Задача 4.6 Задача 4.7 Задача 4.8 Задача 4.1 Винни-Пух и Пятачок договорились утром пойти в гости к Кролику. Пятачок встал пораньше и решил сначала дойти до домика Винни-Пуха, а потом вместе с другом к полудню быть у Кролика. Какое расстояние прошёл Пятачок до полудня, […]

  10513   17.11.2020

Содержание Задача 3.1 Задача 3.2 Задача 3.3 Задача 3.4 Задача 3.5 Задача 3.6 Задача 3.7 Задача 3.8 Задача 3.1 На доске было написано четыре арифметических примера. Маша стёрла числа 1, 2, 3, 4, 5 и написала вместо них буквы (a) Вместо буквы A (1) стояло число 1. (b) Вместо буквы B (2) стояло число 2. […]

  9907   03.11.2020

Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 1 Какая звезда самая яркая на небе Земли? Канопус Вега Полярная Арктур Солнце Денеб Бетельгейзе Сириус Ответ: 5 (2 балла) За ответ (8) – 1 балл.  Комментарий: Солнце – тоже звезда. Задание 2 Назовите тело Солнечной системы, […]

  3885   29.10.2020

Содержание LISTENING READING USE OF ENGLISH Task 1 Task 2 Audioscript Keys LISTENING READING USE OF ENGLISH LISTENING Time: 15 minutes Maximum points – 10 points Прослушайте аудиофайл: For items 1–10 listen to an interview with the astronaut Charles Duke, who is talking about his trip to the moon, and decide whether the statements 1–10 […]

  36684   15.10.2020

Содержание Part 1 «Listening» Part 2 «Reading» Task 1 Task 2 Part 3 «Use of English» Task 1 Task 2 Task 3 Audioscript (Part 1 «Listening») Keys Part 1 «Listening» Part 2 «Reading» Part 3 «Use of English» Part 1 «Listening» Time: 10 minutes Maximum points – 7 How do British people recognize a Russian […]

  36293   06.10.2020

Содержание Part 1 Listening Part 2 Reading Part 3 Use of English Task 1 Task 2 Task 3 Task 4 Audioscript Keys Part 1 Listening Part 2 Reading Part 3 Use of English Part 1 Listening Time: 10 minutes Maximum points – 4 Прослушайте аудиофайл: Listen to the text. Then put four tales in the […]

  39964   29.09.2020

Содержание Part 1 «Listening» (15 minutes) Part 2 «Reading» (40 minutes) Task 1. Questions 1–7 Task 2. Questions 8–15 Part 3 «Use of English» (35 minutes) Task 1. Questions 1–10 Task 2. Questions 11–20 Audioscript Keys Part 1 Listening Part 2 Reading Part 3 Use of English Part 1 «Listening» (15 minutes) Maximum points – […]

  94625   23.09.2020

Содержание Part 1 Listening  (15 minutes) Part 2 Reading (15 minutes) Part 3 Use of English  (30 minutes) Task 1 Task 2 Task 3 Audioscript KEYS Part 1 Listening Part 2 Reading Part 3 Use of English Part 1 Listening  (15 minutes) Maximum points – 5 You will hear a conversation between a boy, Leon, […]

  19330   18.09.2020

Содержание Part 1 (15 minutes) Part 2 «Reading» (15 minutes) Part 3 «Use of English» (30 minutes) Task 1 Task 2 Task 3 Audioscript KEYS Part 1. Listening Part 2. Reading Part 3. Use of English Part 1 (15 minutes) Maximum points – 5 Listening Listen to Helena and her father talking about her school […]

  16525   17.09.2020

Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 1 Что изображено на фотографии? чёрная дыра (первое изображение!) гора Олимп тёмное образование в атмосфере Юпитера солнечное […]

  17030   06.02.2020

Внимание! Первые 6 задач полностью совпадают с первыми 6 задачами заданий по астрономии для 5-7 классов, школьного этапа (1 этап) за 2019-2020 учебный год Содержание Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 7 В центре снимка можно заметить астеризм созвездия Южный крест (он зарисован). В каком полушарии сделана эта […]

  6646   19. 12.2019

загадок для детей с ответами | Простые математические головоломки для развлечения

В жизни ребенка быть умственно активным так же важно, как и физически. Нет ничего лучше загадок, чтобы развлечь мозг самым забавным образом. Большинство детей считают математику кошмаром и довольно трудно. Дайте своему мозгу звездную тренировку с самыми забавными загадками здесь. Проверьте себя и получайте удовольствие от «Загадки на математику для детей» — одного из самых умных способов подойти к предмету.

Использование забавных стратегий при приближении к предмету помогает родителям и учителям пробудить интерес у детей. Выделите время, чтобы решить эти головоломки и сделать свой день лучше. Мы попытались предоставить вам несколько замечательных ответов, чтобы помочь вам. Дети могут легко разгадать эти загадки, если будут проявлять некоторую концентрацию, применять критическое мышление и логические рассуждения.

Загадки на математику для детей

Те, кто любит проверять свои навыки решения проблем, могут попробовать эти математические загадки. Логические головоломки и загадки могут быть полезны для улучшения способностей детей к обучению и навыков решения математических задач.

1. Добавьте число к самому числу, а затем умножьте на 4. Снова разделите число на 8, и вы получите то же самое число еще раз. Что это за номер?

Ответ: Любое число

2. X — нечетное число. Уберите алфавит от X, и он станет четным. Что это за номер?

Ответ: Семь (семерка-S = четное)

3.Тома попросили нарисовать количество табличек на 100 квартирах, что означает, что он должен будет нарисовать числа от 1 до 100. Можете ли вы подсчитать, сколько раз ему придется нарисовать цифру 8?

Ответ: 20 раз. (8, 18, 28, 38, 48, 58, 68, 78, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 98)

4. Во время отправки Том может поместить в картонную коробку 10 маленьких или 8 больших коробок. Всего за одну партию было отправлено 96 коробок. Маленьких ящиков было меньше, чем больших. Какое общее количество коробок он отправил?

Ответ: 11 коробок

4 маленьких коробки (4 * 10 = 40 коробок)

7 больших коробок (7 * 8 = 56 коробок)

Так 96 коробок и всего 11 коробок

5. Если вы покупаете петуха, чтобы откладывать яйца, и рассчитываете получать по три яйца каждый день на завтрак, сколько яиц у вас будет через три недели?

Ответ: Ноль, петухи не откладывают яйца

Математические головоломки и ответы

6.Дед, два отца и два сына вместе пошли в кинотеатр, и каждый купил по одному билету в кино. Сколько всего билетов они купили?

Ответ: 3 (дед тоже отец и отец тоже сын)

7. Если 6 человек построили сарай по 9 часов, сколько времени потребуется 12 людям, чтобы построить такой же сарай?

Ответ: Нет, сарай уже построен!

8. Я — трехзначное число. Моя вторая цифра в 4 раза больше третьей.Моя первая цифра на 3 меньше, чем вторая. Кто я?

Ответ: 141

9. У Раджа 2 книги. Одна из книг перевернута, а вторая поворачивается, так что верхняя часть книги обращена к Раджу. Тогда какова будет общая сумма первых страниц каждой из этих книг?

Ответ: Независимо от того, как книги ориентированы, первая страница каждой книги имеет номер страницы 1, поэтому 1 + 1 = 2.

10. У меня есть фунт перьев и фунт железа? Подскажите, пожалуйста, какая из них больше?

Ответ: Оба они сохраняют тот же вес, что и фунт, независимо от объекта.

Веселые математические загадки для детей с ответами

11. Мобильный телефон и его чехол стоят рупий. Всего 110. Цена мобильного телефона на 100 рупий больше, чем его футляр. Сколько стоит мобильный телефон?

Ответ: 105 рупий (не 110 рупий)

12. Яйца по 0,12 доллара за дюжину. Сколько яиц можно получить за доллар?

Ответ: 100 яиц по пенни за каждое

13. Если вы умножите это число на любое другое, ответ всегда будет таким же.Что это за номер?

Ответ: Ноль

14. Где рыба хранит деньги?

Ответ: На берегу реки.

15. Я добавляю пять к девяти и получаю два. Ответ правильный, но как?

Ответ: Когда 9 утра, прибавьте к нему 5 часов, и вы получите 2 часа дня.

16. Используя только сложение, как можно сложить восемь восьмерок, чтобы получить число 1000?

Ответ: 888 +88 +8 +8 +8 = 1000

17.Как сделать число 7 четным без сложения, вычитания, умножения или деления?

Ответ: Бросьте букву «S» в орфографической семерке.

18. Как вы можете взять 2 из 5 и оставить 4?

Ответ:

F I V E

Уберите две буквы F и E из пяти, и вы получите IV.

19. Сколько сторон у круга?

Ответ: Два. Внутри и снаружи.

20. Сколько раз вы можете вычесть число 5 из 25?

Ответ: Только один раз, потому что после вычитания 25 больше не будет.

Математические загадки с ответами, которые помогут развить разум

Есть много математических загадок, как более простых, так и требующих большой концентрации. Но от их решения вы получаете гораздо большее удовлетворение. С помощью этих головоломок дети могут научиться связывать понятия и развивать нестандартное мышление.

21. Возраст отца и сына в сумме составляет 66 лет. Возраст отца — это возраст сына в обратном порядке. Сколько им может быть лет?

Ответ: Для этого есть три возможных решения: дуэт отец-сын может быть 51 и 15 лет, 42 и 24 года или 60 и 06 лет.

22. Если есть четыре яблока и вы убираете три, сколько у вас есть?

Ответ: Вы взяли три яблока, очевидно, у вас будет три.

23. Вам дают телефон и просят умножить все числа на цифровой клавиатуре устройства. Что будет в ответ?

Ответ: Ноль (поскольку цифровая клавиатура содержит цифру 0, при умножении любого числа на ноль ответ будет нулевым).

24. В зоопарке 100 пар собак.На каждую собаку рождается по две пары малышей. К сожалению, 23 собаки не выжили. Сколько всего собак останется?

Ответ: 977 собак (100 x 2 = 200; 200 + 800 = 1000; 1000 — 23 = 977)

25. В моем ящике для носков 6 черных носков, 8 коричневых, 4 синих и 2 красных носка. Сможете ли вы вычислить минимальное количество носков, которое нужно вытащить, чтобы точно получить подходящую пару?

Ответ: Не менее 5

Простые головоломки по математике для школьников

26.Мужчина вдвое старше своей младшей сестры. Ему тоже вдвое меньше, чем их папе. Через 50 лет возраст сестры станет вдвое меньше возраста их отца. Какого возраста сейчас мужчина?

Ответ: Ему 50 лет.

27. У Рави двое детей. Если старший ребенок — мальчик, то какова вероятность того, что его второй ребенок также будет мальчиком?

Ответ: 50 процентов

28. В рейс вышли два самолета. Один рейс летит из Лондона в КЛ со скоростью 400 миль в час.Другой рейс летит из КЛ в Лондон со скоростью 600 миль в час. Оба этих полета встретились в одной точке. Какой из этих рейсов будет ближе к KL?

Ответ: Оба рейса при встрече будут находиться на одинаковом расстоянии от KL.

29. Есть пустая корзина диаметром один фут. Можете ли вы назвать общее количество яиц, которое вы можете положить в эту пустую корзину?

Ответ: Только одно яйцо, когда вы кладете яйцо, корзина больше не остается пустой.

30. 1 = 3, 2 = 3, 3 = 5, 4 = 4, 5 = 4, 6 = 3, 7 = 5, 8 = 5, 9 = 4, 10 = 3, 11 =? 12 =? Сможете ли вы завершить последовательность?

Ответ: 6. Присутствующие числа представляют количество букв в написании соответствующего числа.

Сложные математические загадки с ответами

31. Предположим, 1 + 9 + 8 = 1, тогда что может быть 2 + 8 + 9?

Ответ: 10! (Рассмотрим первую букву написания каждой цифры: Один + Девять + Восемь = ОДИН, аналогично Два + Восемь + Девять = ДЕСЯТЬ).

32. Сэм родился 1 января 23 г. до н. Э. в городе КЛ и скончался 2 января 23 года нашей эры. Сколько ему лет было, когда он умер?

Ответ: 45 лет! В фактических расчетах в обоих периодах 23 года, но нет нулевого года. Таким образом, вы можете сложить эти периоды и вычесть 1 год. Это означает, что 23 + 23 — 1 = 45 лет.

33. Две курицы могут отложить два яйца за две минуты. Если это максимально возможная скорость, какое общее количество кур нужно, чтобы получить 500 яиц за 500 минут?

Ответ: 2 куры

34.Петра спросили, сколько ему лет. Его ответ был таким: «Через 2 года мой возраст будет вдвое старше, когда вы спросили об этом пять лет назад». Сколько ему лет?

Ответ:

Пусть возраст Петра будет X лет

Х + 2 = 2 (Х-5)

Х + 2 = 2Х-10

Х = 12

35. 100 девушек пришли на вечеринку. У 85 из них была красная сумка, 75 из них были в коричневых туфлях, 60 из них пришли с зонтиком, а 90 девочек носили кольцо. У скольких девушек были все эти четыре предмета?

Ответ: 10

Разделить на 3.У всех девушек было по три предмета. Остаток указывает количество девочек с 4 пунктами.

85

75

60

90

36. 100 монет упали и рассыпались в темном месте. 90 монет упали орлом вверх, а остальные 10 монет выпали решкой вверх. Вам предлагается разделить эти монеты на 2 стопки. Однако в каждой стопке должно быть одинаковое количество монет, находящихся решкой вверх. Как это возможно?

Ответ: Во-первых, все сваи не обязательно должны быть одинакового размера.Я могу сделать 2 стопки, одну по 90 монет, а другую по 10 монет. Теперь просто переверните все 10 монет в стопку. Таким образом, в стопках будет одинаковое количество хвостов.

Математические загадки и головоломки

37. Робин подбрасывает монету 10 раз, и все десять раз она приземляется в положении один на один. Так каковы возможные шансы, что он снова подбросит его и окажется в хедз-ап позиции?

Ответ: У него 50% шанс увидеть хедз-ап позицию. Это потому, что подбрасывание монеты не зависит от первых 10 подбрасываний.

38. Мэри купила на день рождения ребенка круглый торт и увидела в доме 6 неожиданных гостей. Поэтому ей пришлось разрезать торт на 8 частей. Поскольку ее ребенку было 3 года, они настояли на том, чтобы во время празднования на торте сделали 3 надреза. Как она может сделать это возможным?

Ответ: Рассмотрим среднюю точку торта в вертикальном положении. Разрежьте по горизонтали, пока он не достигнет той же точки снова, сделав ровно половину. Второй разрез должен быть сделан вертикально, проходя через два круглых коржа.Получается 4 лепешки. Теперь сделайте горизонтальный разрез аналогичным образом, а затем снова разрежьте эти 4 части пополам, в результате чего получится 8 частей.

39. Цена утки составляет рупий. 9, паук стоит рупий. 36, а пчела стоила рупий. 27. С учетом этой информации, какова будет цена кошки?

Ответ: 18 рупий (4,50 рупий за ногу)

Глупые математические головоломки с ответами

40. 1/2 из 2/3 из 3/4 из 4/5 из 5/6 из 6/7 из 7/8 из 8/9 из 9/10 из 10 000.Можете ли вы решить эту проблему за один шаг?

Ответ: 1000! 1/10 от 10 000 дает 1000. (Все обнуляется, если вы умножите все эти дроби, а оставшаяся часть будет 1/10)

41. Семь мальчиков встретились на вечеринке. Каждый из них только один раз пожимает друг другу руки. Каково общее количество имевших место рукопожатий?

Ответ: Двадцать один

42. У Амира с собой 2 ведра. В первом ведре были только красные шарики, а в другом — только коричневые шарики.В двух ведрах одинаковое количество шариков. Что он может сделать, чтобы увеличить вероятность вытаскивания красного шарика из каждого ведра?

Ответ: Храните только один красный шарик в одном ведре, а оставшиеся красные и коричневые шарики в другом ведре. Это увеличивает его шансы схватить красный шарик из каждого ведра (примерно 75%), что невозможно при любом другом расположении.

43. Том шел в парк KLCC. Он встретил парня с 7 женами, и каждая из них пришла с 7 мешками.Все эти мешки содержат 7 кошек, и у каждой из этих 7 кошек было по 7 комплектов. Итак, сколько в общей сложности собрались в KLCC Park?

Ответ: 1. В парк KLCC собирался только Том.

44. На моей книжной полке определенное количество книг. Я взял книгу, шестую справа и четвертую слева. Вы можете узнать количество книг на моей полке?

Ответ: 9 ((6 + 4) -1. Или вы просто разложите набор из 10 книг и посмотрите, как это работает)

Веселые загадки на математику для детей с ответами

45.У Марии 7 дочерей, у каждой из них есть брат. Можете ли вы подсчитать общее количество детей у Мэри?

Ответ: 8 детей, потому что у сестер всего один общий брат.

46. Маленький мальчик ходит по магазинам и покупает 12 помидоров. По дороге домой все, кроме 9, разоряются и разоряются. Сколько помидоров осталось в хорошем состоянии?

Ответ: 9

47. Если бы у вас было пять манго и два банана в одной руке и два манго и четыре банана в другой руке, что бы вы ели?

Ответ: Очень большие руки

48.Когда-то было семь гномов, которые все были братьями. Все они родились с разницей в два года. Самому младшему карлику семь лет. Сколько лет его старшему брату?

Ответ: Старшему брату 19 лет.

49. На чужой земле далеко половина от 10 равна 6. Если та же пропорция верна, то какова 1/6 часть от 30 на этой чужой земле?

Ответ: 6

50. Как сложить восемь четверок, чтобы в сумме получилось 500?

Ответ: 444 + 44 + 4 + 4 + 4 = 500

Заключение

Math Riddles Здесь не только вызовут нестандартное мышление ваших детей, но и проверит их логическое мышление.Эти простые и забавные головоломки могут стать отличным развлечением для ваших детей. Детям будет очень весело и они будут придумывать нестандартные и креативные решения.

Поделитесь ею со своими близкими, если считаете, что статью стоит прочитать. Добавьте наш сайт в закладки, чтобы увидеть больше таких интересных и удивительных математических загадок, вопросов GK и т. Д.

Если: JK = 6x + 2, KL = 7 + 4, и JL = 45, Найдите KL. J K L

Напишите уравнение квадратичной функции с корнями в точках -6 и -5 и вершиной в точках (-5.5, -0,25). Напишите уравнение в стандартной форме. на

Классифицируйте следующий треугольник. Проверить все, что относится.

Напишите уравнение квадратичной функции с корнями в точках 6 и 2 и вершиной в точках (4, -4/3). Напишите уравнение в стандартной форме.

Может ли кто-нибудь решить 0/2 + 3,4 = 12,4

Запишите в вершинной форме уравнение квадратичной функции с вершиной в (-2, 1) а и точка (-4, -3).

Ракетный клуб запускает модели ракет.Стартовая площадка находится на высоте 30 футов над землей. Ваша модель ракеты имеет начальную вертикальную скорость 105 f. … eet в секунду. Модель ракеты вашего друга имеет начальную вертикальную скорость 100 футов в секунду. Сравните графики. Через сколько секунд ваша ракета поднимется на высоту 119 футов над землей? Округлите ответ до ближайшей десятой. Объясните разумность своих ответов.

Холодным январским утром температура жидкости в радиаторе в грузовике Кристины составляет –13 ° F. При включенном двигателе температура повышается в 3 раза.6 ° F в минуту. Сколько … температура радиатора должна достигнуть 50 ° F? Какое выражение говорит о том, насколько температура должна измениться с -13 ° F до 50 ° F? Какое выражение говорит о том, сколько времени потребуется, чтобы температура изменилась? За сколько времени изменится температура? ПОЖАЛУЙСТА ПОМОГИ!! Мне он нужен для выполнения задания по краю.

Определите матричное преобразование AKLM, имеющее координаты K (-2, 3), L (-4, -2) и M (-3,0), для отражения по оси x.Затем определите … правильные вершины изображения

Джо практиковал на трубе 53 минуты в день в течение 20 дней. Чарльз упражнялась на трубе по 35 минут в день в течение 30 дней. Какие высказывания о Джо и … d Char верны? Выбрать все, что подходит. А. Джо тренировался в общей сложности 1530 минут. Б. Чарльз тренировался в общей сложности 1050 минут. С. Вместе Джо и Чар тренировались 2580 минут. Д. Вместе Джо и Чар тренировались 2110 минут.

Как найти конечные точки отрезка

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Числовые привязки влияют на ответы на математические уравнения

Предвзятые вычисления: числовые привязки влияют на ответы на математические уравнения

Суждение и принятие решений, т. 6, вып. 1, февраль 2011 г., стр. 139-146

Эндрю Р. Смит * Пол Д. Виндшитл #

Людям часто приходится выполнять вычисления, чтобы получить числовые оценка (например, покупатель в продуктовом магазине оценивает общую цену содержимого его или ее корзины покупок). Текущие исследования были предназначен для проверки того, являются ли оценки, основанные на расчетах, под влиянием сравнений с нерелевантными якорями. Предыдущий исследования показали, что оценки по широкому кругу контексты ассимилируются с якорями, но ни один из них не изучал оценки на основе расчетов.В двух исследованиях участники сравнивали ответы на математические задачи с якорями. В обоих исследованиях оценки участников ассимилировались с якорными ценностями. Этот эффект был смягчен ограничением по времени, так что эффекты привязки были больше, когда способность участников участвовать в расчетах был ограничен ограниченным сроком.

Ключевые слова: привязка, систематическая ошибка, эвристика, вычисления, математика, числовые значения. грунтовка, грунтовка по величине.

1 Введение

При вычислении числовых оценок люди часто сталкиваются с как актуальная, так и нерелевантная информация.Например, продуктовый магазин покупатель, который пытается подсчитать общую стоимость своей тележки с продуктами содержание может увидеть, что новый газовый гриль продается по цене 199,99 долларов. Воля на оценку покупателя влияют нерелевантные стоимость нового гриля? Или, в более общем плане, люди находятся под влиянием нерелевантные числовые значения (т. е. якоря) при вычислении числовых оценки?

Многочисленные исследования показали, что оценки имеют тенденцию ассимилироваться. к нерелевантным якорям (обзор см. в Chapman & Johnson, 2002).Например, эффекты привязки наблюдались с общими вопросы знаний, такие как длина реки Миссисипи и высота Эвереста (Jacowitz & Kahneman, 1995), преступник предложения (Englich, Mussweiler, & Strack, 2006) и исполнение рейтинги профессоров университетов (Торстейнсон, Брейер, Этвелл, Гамильтон и Приветт, 2008). Как видно из приведенных выше примеров, типичное исследование привязки требует, чтобы участники набирали информацию из памяти и / или произвести количественную оценку из преимущественно неколичественная информация.В текущих исследованиях мы исследовал эффекты привязки в другом контексте — в том, где участникам необходимо было выполнить расчет, чтобы сгенерировать свои оценивать. Несмотря на то, что подобные ситуации довольно распространены (например, оценка общей стоимости нескольких продуктов, подсчет калорий потребляется за день, в расчете на примерный газ пробег), мало что известно о том, как якоря влияют на оценки, сделанные из расчетов.

Существует классическое исследование, которое часто приводят в качестве примера привязка к расчетам, а именно исследование Тверски и Канемана (1974), в котором участники дали более низкие оценки произведения 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8, чем 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1.Однако, хотя этот вывод служит иллюстрацией того, что привязка может повлиять на расчетные ответы, это идиосинкразический пример в что потенциальные якоря (т. е. первые числа в серии) часть самих выражений. Также якоря информативны что касается ответа на выражение — опять же, потому что якоря часть проблемы. Следовательно, иллюстрация не обязательно поговорить о том, является ли нерелевантный якорь внешним по отношению к выражение может повлиять на ответы людей.

Представьте, что человеку нужно решить «728 + 136 + 545 =?» и имеет недавно был показан нерелевантный номер, например 824. Было бы так значение привязки, которое оказывается меньше фактического ответа, иметь какое-либо предвзятое влияние на решение проблемы человеком? Два наиболее известных объяснения эффектов привязки не помогли бы похоже, предсказывает эффект якоря. Во-первых, отборных доступность объяснения эффекта привязки не кажутся имеет прямое отношение к возможности нахождения привязки с помощью математики проблемы (Mussweiler & Strack, 1999; Strack & Mussweiler, 1997; см. также Chapman & Johnson, 1999).Эти учетные записи предполагают, что когда участники сталкиваются с якорем (например, «Река Миссисипи длиннее или короче 5000 миль? »), они сначала проверяют, target равно значению привязки (например, «Река Миссисипи 5000 миль? »). Потому что люди склонны выдвигать гипотезы последовательное тестирование, они будут набирать информацию, которая является последовательной с целью, равной якорю. Выборочная доступность учетные записи предполагают, что активированная информация семантически связана привязке к значению (Mussweiler & Strack, 2000, 2001).Когда участники генерируют свою окончательную оценку, они используют этот предвзятый набор доступных информация для информирования их оценки. Хотя выборочный доступность может объяснить эффекты привязки во многих ситуациях, потому что учетная запись основана на предвзятом наборе информации от памяти, похоже, это неприменимо к ситуациям, когда люди выполнение расчета на основе доступной информации. Более того, потому что учетные записи выборочной доступности предполагают, что якоря увеличивают доступность семантически связанной информации, у них есть сложность объяснения эффектов привязки с помощью чисто числовых информация — как было использовано в текущих исследованиях.

Второй счет, привязка и недостаточная регулировка (Эпли & Гилович, 2001, 2004, 2005, 2006; Тверски и Канеман, 1974), предлагает набор процессов, которые не кажутся приемлемыми для объяснения того, как якоря могут повлиять на решение математических задач. Недостаточный корректировочные счета предполагают, что участники используют якорь в качестве отправная точка, а затем откорректировать их оценку от привязки ценить. Трудно представить, почему и как можно было бы начать оценка на якоре, одновременно решая математическую задачу.Кроме того, все якоря в текущих исследованиях были внешними. при условии, и процесс корректировки, как предполагается, происходит только от самогенерируемый якорь (Эпли и Гилович, 2001, 2004, 2005, 2006).

Хотя ни выборочной доступности, ни недостаточности корректировочные счета, казалось бы, предсказывают эффект нерелевантных якоря по ответам на математические задачи, есть два дополнительных аккаунта которые больше поддаются такому предсказанию. Числовой Начальные значения величин и В аккаунтах утверждается, что якоря начальные числа или величины, аналогичные значению привязки.Например, Произвольные идентификационные номера участников повлияли на их оценку количество врачей в телефонной книге (Wilson, Houston, Etling и Брекке, 1996). Предположительно, просмотр идентификационного номера увеличил доступность похожих номеров. Когда участники сгенерировали свои по оценкам, эти цифры со штрихом чаще приходили на ум, тем самым влияя на их оценки (см. также Critcher & Gilovich, 2007; Вонг и Квонг, 2000). Счет начального значения магнитуды аналогичен, но вместо начальных чисел предполагается, что якоря простаивают понятия величины (например,g., «большой», «маленький») и эти понятия влияют на оценки, которые дают люди (Oppenheimer, LeBoeuf, & Брюэр, 2008). Например, в одном исследовании рисование длинной линии вызывало участники дают более длинные оценки длины Миссисипи Ривер по сравнению с участниками, нарисовавшими короткую линию.

В основе нашего прогноза лежат числовые и магнитные первичные расчеты. что нерелевантные якоря повлияют на ответы на математические задачи. В частности, мы предлагаем, чтобы, если расчеты, требуемые математические задачи просты, люди часто генерируют приближение отвечать.То есть, хотя они могут применять некоторые математические правила, люди также выбирают ярлыки и оценивают, а не строго вычислить. Когда люди используют этот тип стратегии, якоря будут оказывать смещающее влияние посредством числового или магнитного прайминга. Что то есть оценки участников будут ассимилироваться с ценностями или величины, которые становятся доступными с помощью якорей. Например, если человек подвергается высокому якорю (например, 6 245), это значение может увеличить активацию числовых значений возле якоря (Wilson et al. al., 1996) или связанных величин (например, «большой» или «большой»; Оппенгеймер и др., 2008). Затем, вычисляя ответ на математическая задача (например, 234 + 798 + 912), оценка человека может ассимилироваться к ценности или величине, которые стали доступными.

В обоих наших исследованиях участники отвечали на математические задачи после сравнения с якорями. Потому что у участников были все информация, необходимая им для объективных оценок, была возможно, что участники будут использовать исключительно стратегии расчета и поэтому приходят к правильным, беспристрастным ответам. Однако мы использовали временные рамки, которые заставляли участников работать быстро. Мы предположили, что ограничения по времени в 15 секунд будет достаточно, чтобы запретить большинству участников используя чистую и точную стратегию расчета. Важный вопрос будет ли отклонение от фактических решений систематически смещен в сторону значения привязки. В В дополнение к условию с 15-секундным ограничением мы также включили состояние с более жесткими временными рамками (4 секунды в Исследовании 1 и 5 секунд в Исследование 2).Это позволило нам проверить, работают ли эффекты якоря. значение станет сильнее по мере увеличения нехватки времени. Этот образец согласуется с идеей о том, что, поскольку необходимость оценки (скорее чем формально рассчитать) увеличивается, вероятность смещения от внешние анкеры также увеличиваются. Альтернативный шаблон данных также правдоподобно, однако. А именно, цейтнот может просто увеличиться ошибка — но не систематически в направлении якоря.

2 Исследование 1

2.1 Метод

2.1.1 Участники и дизайн

Семьдесят пять студентов из Университета Айовы поступили в вводный курс психологии участвовал как частичное выполнение их исследовательские требования. Это исследование было 2 (Якорь: высокий / низкий) x 2 (Ограничение по времени: 4/15 секунд) x 2 (Порядок ограничения по времени: сначала 4 секунды / сначала 15 секунд) смешанная модель с привязкой и ограничением по времени, как внутри субъектов, факторов и временное ограничение как фактор между субъектами. Срок действия ордера сделал не влияет на оценки ни в одном из исследований, поэтому этот фактор не будет обсуждается далее.

2.1.2 Вопросы по математике и привязки

Все вопросы по математике, которые видели участники, имели форму «X ₁ + X ₂ + X ₃ = Y». Чтобы создать эти вопросы, три числа (например, X ₁ , X ₂ и X ₃ ) были сгенерированы случайным образом для каждого испытания так, чтобы решение (т. е. Y) находилось между 1100 и 1900. ¹ Значения привязки также были случайным образом определяется для каждого испытания; низкие якоря были между 700 и 900 и высокие якоря находились между 2100 и 2300 годами.Например, участник может возникнуть вопрос, будет ли ответ на «728 + 136 + 545 =?» больше или менее 824 в состоянии низкого якоря или 2192 в состоянии высокого якоря состояние.

Вопросы привязки были сгруппированы в два блока. В Уравновешенный порядок, участники ответили на один блок вопросов с ограничением времени в 4 секунды, а другой блок с ограничением времени в 15 секунд предел. В каждом блоке участники увидели по три высоких и три низких якоря. вопросы в случайном порядке. Всего участники ответили на три вопросы в каждом из четырех условий (высокий якорь, 4-секундное время предел; высокий якорь, ограничение по времени 15 секунд; низкий якорь, ограничение по времени 4 секунды; низкий якорь, ограничение по времени 15 секунд).В дополнение к этим критическим вопросы, участники также ответили на четыре вопроса-заполнителя. В задачи наполнителя были идентичны для всех участников и имели якоря которые были близки к реальным ответам на математические задачи. Мы включили элементы-наполнители, чтобы снизить вероятность того, что участники узнают что якоря были либо высокими, либо низкими.

2.1.3 Процедура

Участников проинструктировали, что они будут отвечать по математике. уравнения на компьютере, и у него было бы очень мало времени, чтобы просмотреть каждое уравнение.Поэтому они должны работать максимально быстро и как можно точнее. Участники впервые ответили на 10 упражнений математические проблемы. Например, участник может увидеть уравнение «435 + 587 + 298 =?» с текстовым полем ниже, чтобы ввести ответ на уравнение. Через 4 секунды уравнение было стерто из экран, но поле для ввода текста осталось. Однажды участник введя свой ответ, он перешел к следующей задаче.

После ответов на практические задачи участникам сказали, что они будут решать еще несколько математических задач в два этапа.В частности, им сказали, что сначала они увидят уравнение и сравните ответ уравнения со «случайно сгенерированным числом». Во-вторых, они дадут ответ на уравнение. В затем участникам был показан пример, чтобы убедиться, что они поняли их задача. Затем им сказали, что у них будет небольшое количество время для просмотра каждого уравнения, поэтому они должны работать как можно быстрее и как можно точнее. Наконец, им сказали, что если они неуверенные в точном ответе на уравнение, они должны предоставить свои лучшая оценка.

Каждое испытание начиналось с представления значения привязки (например, «Is ответ на следующее уравнение меньше или больше 784? »). После задержки в 3 секунды было отображено уравнение (например, «564 + 298 + 712 ”). Участники указали, был ли ответ на уравнение был больше или меньше якоря, а затем ввел свою оценку ответа на уравнение.

В зависимости от условия ограничения по времени уравнение отображалось для либо 4, либо 15 сек. Таймер обратного отсчета в правом нижнем углу на экране отображается количество секунд, оставшихся до уравнения был стерт.После того, как участники ответили на вопросы в первом блока, им сказали, что лимит времени меняется (с 4 до 15 секунд, или наоборот), а затем ответил на вопросы во втором блоке.

2.2 Результаты

2.2.1 Предварительный анализ

Трое участников были исключены из анализа, поскольку их ответы показали, что они не пытались предоставить точные ответы. Мы также удалили небольшое количество оценок (7/864 или <1%), что, скорее всего, было вызвано опечатками (например,г., оценки ниже 100 и выше 10 000). Что касается сравнительных суждений, участники правильно определили, был ли ответ на уравнение был больше или меньше якоря в 94,3% испытаний. Точность этих суждений не различалась в зависимости от привязки или времени. условия давления. Всего 59 из 72 участников (81,9%) ответил как минимум на 11 из 12 сравнительных суждений правильно. ² Относительно точности окончательные ответы участников на математические задачи, только 0.2% и 11,1% окончательных ответов были точно правильными за 4 секунды. и 15 секунд соответственно. Использование более мягкого критерия для точности, мы обнаружили, что только 3,0% и 18,5% окончательных ответов были в пределах 5 единиц от правильного ответа в двух условиях, соответственно. Эти результаты согласуются с нашим предположением о том, что Ограничения по времени в 15 секунд обычно достаточно, чтобы запретить участникам от использования чистой и точной стратегии расчета. Они также предлагают эти 4 секунды были еще более ограничивающими для такой стратегии.

2.2.2 Основные анализы

Ключевой вопрос сейчас в том, будут ли финалы участников ответы показали бы значительный уклон в сторону якорей. Второстепенный вопрос заключался в том, будет ли этот эффект усилен по мере того, как давление времени увеличилось с 15 секунд до 4 секунд.

Поскольку каждая математическая задача генерировалась случайным образом для каждого участника, фактические ответы на проблемы могут случайно отличаться в зависимости от условия. Поэтому по каждому из 12 вопросов привязки мы рассчитал отклонение оценки каждого участника от фактический ответ на уравнение, а затем усреднить три оценки отклонения в пределах заданного условия.Необходимо отметить, что анализы, проведенные на основе необработанных оценок участников, не существенно отличаются от проведенных по своим показателям отклонения. Мы провели анализ повторных измерений 2 (якорь) x 2 (срок). дисперсии (ANOVA) оценок отклонения участников.

Самое главное, что был предсказанный основной эффект якоря, F (1, 71) = 17,16, p <0,001, частичное η ² = 0,20. Участники дали более высокие оценки после воздействие более высокого якоря, чем низкого якоря.Также был основной эффект ограничения по времени, F (1, 71) = 9,28, p = 0,003, частичный η ² = 0,12; участники дали более высокие оценки в 15-секундном состоянии. Ограничение по времени основного эффекта не было воспроизведен в исследовании 2, поэтому мы не будем его подробно обсуждать. Два основные эффекты были квалифицированы как незначительное взаимодействие, F (1, 71) = 3,42, p = 0,07, частичное η ² = 0,05. Для простоты интерпретации рисунок 1. отображает среднюю оценку участников для каждого условия, а не их оценки отклонения.Как видно на рисунке 1, участники на оценки в большей степени повлияли значения привязки в условие 4 секунды по сравнению с условием 15 секунд. Хотя эффект привязки был больше в 4-секундном режиме, простые эффекты тесты выявили значительные эффекты закрепления как в 4-секундных интервалах. условие, F (1, 71) = 13,79, p <0,001, частичное η ² = 0,16 и условие 15 с, F (1, 71) = 6,55, p = 0,01, частичное η ² =.08.

Рис. 1. Средние оценки участников исследования 1 в зависимости от якорные и временные ограничения. Планки погрешностей представляют ± 1 SE.

2.3 Обсуждение

Результаты исследования 1 показывают, что ответы участников на математические на проблемы повлияли значения привязки. То есть их оценки ассимилирован к значению якоря. Как обсуждалось ранее, это кажется, что эффекты привязки, наблюдаемые в этой конкретной парадигме должен управляться числовым или амплитудным затравкой.Предположительно, разоблачение к значению привязки увеличена доступность чисел или величины аналогичны якорю, и это увеличение активации повлияли на оценки участников.

Еще один интересный результат — эффект привязки был больше. когда участники находились в более затруднительном положении. Есть две тесно связанные характеристики этого взаимодействия. Одна из возможностей состоит в том, что привязки влияли на оценки аналогичным образом в оба условия ограничения по времени, за исключением времени, когда участники смогли буквально вычислить свой окончательный ответ.Второй возможно, что даже среди набора оценок, которые не были достигается за счет полного расчета, цейтнот привел к увеличению влияние якорей. Обе эти характеристики совместимы с нашими общими аргументами. Результаты исследования 1 несколько неоднозначный, на котором более справедливо. Если мы удалим все ответы, были в пределах 5 единиц от правильного ответа (что исключает 3,0% и 18,5% ответов в условиях 4 и 15 секунд), результаты для взаимодействия с ограничением времени привязки X изменяются незначительно, F (1, 69) = 2.32, p = 0,13, частичное η ² = 0,03. Это говорит о том, что даже среди множества оценки, которые не были достигнуты путем полного расчета, время давление имеет значение. Результаты исследования 2 дают более четкий вывод. по этому поводу.

3 Исследование 2

Хотя результаты Исследования 1 согласуются с числовыми или Есть альтернативное объяснение. Это возможно, что, хотя якоря были описаны как «случайно сгенерировано », участники рассматривали значение привязки как информативное к их оценке или как намек на реальные ответы (Schwarz, 1994).В исследовании 2 мы использовали экстремальные привязки, чтобы снизить вероятность что участники будут рассматривать их как информативные или возможные ответы на уравнения. Если эффекты привязки, наблюдаемые в исследовании 1 из-за того, что участники рассматривали якоря как информативные, используя крайние анкеры должны устранять или уменьшать эффекты анкеровки. Однако, поскольку крайние якоря все еще могут действовать как простые числа, числовые и количественные первичные счета предсказывают, что участники будут демонстрируют эффект привязки даже при экстремальных значениях привязки.

Стоит также отметить, что математические задачи в Уроке 2 были больше сложнее, чем в Исследовании 1, что еще больше снизило способность участникам использовать стратегию чистого расчета, даже для 15 условие sec.

3.1 Метод

3.1.1 Участники и дизайн

Тридцать два студента из Университета Айовы поступили в вводный курс психологии участвовал как частичное выполнение их исследовательские требования. Это исследование было 2 (Якорь: высокий / низкий) x 2 (Ограничение по времени: 5/15 секунд) x 2 (Порядок ограничения по времени: сначала 5 секунд / сначала 15 секунд) смешанная модель с привязкой и ограничением по времени, как внутри субъектов, факторов и временное ограничение как фактор между субъектами.

3.1.2 Математические вопросы и якоря

Как и в первом исследовании, математические вопросы имели форму «X ₁ + X ₂ + X ₃ = Y». В этом исследовании сумма чисел была случайным образом определена как от 4000 до 8000. Низкие якоря были между 500 и 999. в то время как высокие якоря находились между 11 001 и 11 500. Например, участника могут спросить, будет ли ответ на «1964 + 1297 + 2636 =?» более или менее 783 в нижнем якорном состоянии или 11 243 в высокое состояние якоря.

3.1.3 Процедура

Процедуры были такими же, как в Исследовании 1, за исключением: 1) более экстремальных использовались якоря, 2) не было вопросов по практике, и 3) время предел в условиях нижнего предела был 5 секунд, а не 4 секунды.

3.2 Результаты и обсуждение

3.2.1 Предварительный анализ

Сначала мы удалили небольшое количество оценок (7/384 или <2%) что, скорее всего, произошло из-за опечаток (например, оценки ниже 1000 и свыше 15000). В среднем участники ответили 95.3% от сравнительные суждения правильно. Точность не различалась в зависимости от якорные или временные условия давления. Всего 28 из 32 участников (87,5%) ответили как минимум на 11 из 12 сравнительных оценок правильно. По поводу точности финала участников ответы на математические задачи, ни один из ответов не был в точности правильным в условиях 4 секунд и только 2,1% были правильными в течение 15 секунд состояние. Даже при использовании более мягкого критерия точности ни один окончательных ответов в условии 4 секунды и только 3.7% из 15 sec были в пределах 5 единиц от правильного ответа. В качестве предполагалось, участникам было довольно сложно точно вычислить ответы на математические задачи как в цейтноте условия.

3.2.2 Основной анализ

Как и в исследовании 1, мы создали оценки отклонений от участников оценки. Затем мы провели 2 (якорь) x 2 (ограничение по времени) ANOVA с повторными измерениями оценок отклонения участников. В ANOVA выявил предсказанный главный эффект якоря, F (1, 31) = 13.71, p = 0,001, частичное η ² = 0,31. Опять же, участники дали более высокие оценки после воздействия высокий якорь, а не низкий якорь. В отличие от исследования 1, не было основной эффект ограничения времени, F (1, 31) = 2,43, p = 0,13, частичное η ² = 0,07. Однако был значимый якорь X ограничение времени взаимодействия, F (1, 31) = 6.06, p = 0,02, частичное η ² = 0,16. Как может быть Как показано на Рисунке 2, на оценки участников повлияли значения привязки в большей степени в условии 5 секунд, чем в Состояние 15 сек.Тесты простых эффектов выявили значительную привязку эффекты в условиях 5 секунд, F (1, 31) = 12,40, p = 0,001, частичное η ² = 0,29 и почти значительный эффект закрепления в условиях 15 секунд, F (1, 31) = 3,41, p = 0,07, частичное η ² = 0,10.

Рисунок 2: Средние оценки участников исследования 2 в зависимости от якорные и временные ограничения. Планки погрешностей представляют ± 1 SE.

Таким образом, участники исследования 2 продемонстрировали устойчивые эффекты привязки. при использовании довольно экстремальных анкеров.Кажется маловероятным, что участники интерпретировали крайние якоря как полезную информацию, но влияние якорей в исследовании 2 было в основном таким же, как и в исследовании 1. Эффекты привязки снова были смягчены давлением времени с более жесткое ограничение по времени, приводящее к большему эффекту привязки. Даже когда мы удалили все ответы, которые находились в пределах 5 единиц от правильный ответ, результаты взаимодействия с привязкой X по времени остается значимым, F (1, 31) = 5,64, p =.02, частичное η ² = 0,15. Это показывает, что даже среди набор оценок, которые не были достигнуты путем полного расчета, нехватка времени увеличивает эффекты привязки.

4 Общее обсуждение

Два ключевых аспекта привязки — выборочная доступность и недостаточная корректировка — можно предположить, что якоря не будут влиять оценки людей, основанные на расчетах. С другой стороны, числовые и количественные первичные счета предсказывают эффект. В соответствии с этим прогнозом мы обнаружили, что нерелевантные якоря повлияли на ответы участников по математике проблемы.Еще одним важным открытием стало ограничение способность участников использовать предоставленную информацию увеличили величину эффектов привязки. Наконец, этот эффект сохранялись даже тогда, когда якоря были крайними по сравнению с ответами на математические задачи.

4.1 Почему давление времени увеличило анкеровку?

В ряде исследований было обнаружено, что эффекты закрепления извне при условии, что якоря невосприимчивы к манипуляциям с когнитивной нагрузкой (например, Эпли и Гилович, 2006; Mussweiler & Strack, 1999).Следовательно, это может показаться странным, что нехватка времени усилила эффекты привязки в нашем исследования. Однако мы предположили, что что люди часто выполняют минимальные вычисления, а затем оценивают свои окончательный ответ. Помещение людей в экстремальный цейтнот несомненно, снижает способность людей рассчитывать точный ответ и повышение склонности к оценке ответа. В В свою очередь, это увеличит смещающее влияние якорей.

Наши результаты также согласуются с недавним исследованием, демонстрирующим эффекты привязки, вызванные числовым или магнитным затравкой (Blankenship, Wegener, Petty, Detweiler-Bedell, & Macy, 2008, эксперимент 4).В частности, отвечая на общие вопросы, участники проявлял значительный эффект закрепления при высокой когнитивной нагрузке, но без эффекта привязки при низкой когнитивной нагрузке. В соответствии с Бланкеншип и др., Это произошло потому, что при высоких уровнях нагрузки, участники не смогли набрать значительное количество соответствующая информация из памяти, чтобы вызвать их ответ и были, следовательно, под влиянием количества или величины, которые были сделаны доступны по якорям.

4.2 Что было штриховкой: числа или величины?

Наши исследования не предназначались для определения того, является ли числовое значение или величина грунтовка была более ответственна за наблюдаемые эффекты. Однако мы можем размышлять об этом вопросе. Многочисленные исследования показали, что числовые простые числа могут влиять на числовую обработку (например, Brysbaert, 1995; den Heyer & Briand, 1986). Например, такое число, как 66, называется быстрее, если ему предшествует близкое число (65), чем дальнее число (52).Кроме того, сравнения между целевым показателем и конкретным стандартом быстрее, когда простое число похоже на цель, а не отличается (Koechlin, Naccache, Block, & Dehaene, 1999). Учитывая эти результаты, кажется возможным, что числовые якоря могут простаивать числа, относящиеся к значение привязки.

Однако есть две причины, по которым грунтовка по величине может лучше служить как объяснение эффектов, наблюдаемых в текущих исследованиях. Во-первых, большинство исследователей сходятся во мнении, что в отношении конкретных процесс числового прайминга, числа, состоящие из трех или более цифр, сводятся к их составляющим, а не обрабатываются целостно (обсуждение см. в Ratinickx, Brysbaert & Fias, 2005).Следовательно, число вроде 1313 может сделать больше для простоты числа 2. чем число 1,657. Во-вторых, числовые эффекты прайминга не обычно простираются очень далеко (Reynvoet & Brysbaert, 1999; Reynvoet, Brysbaert, & Fias, 2002). Например, при использовании замаскированных простых чисел праймирование с помощью 1 может облегчить распознавание 2, но не 9. Результаты Reynvoet and Brysbaert (1999) показывают, что цифры не простые значения более чем на 3 от основного. В текущих исследованиях якоря всегда были больше чем двузначные числа и оценки, которые дали участники как правило, сильно отличались от значений привязки.Следовательно, это кажется маловероятным, что строгое числовое праймирование, по крайней мере, как оно определено в когнитивной литературе по числовому праймингу может объяснять наблюдаемые эффекты привязки. Вариант числового прайминга может все еще считается жизнеспособным, если более либеральное определение числового использовались грунтовки, в которых категории чисел могли быть начерчены (например, «верхние сотни», «нижние тысячи»).

Также жизнеспособным является первичное объяснение величины, впервые предложенное Оппенгеймер и др. (2008).В одном из своих этюдов длинный линия заставила участников дать более высокие оценки длины Река Миссисипи. В другом исследовании рисование длинных линий увеличивало вероятность того, что участники заполнили фрагмент слова _все чтобы сформировать высотой . Предположительно, рисование длинной линии грунтовано связанными величины, и эти величины повлияли на оценки и результативность участников на слове завершение задачи. Подобно эффекту рисования длинных или коротких линий, кажется вполне возможным, что якоря увеличили активацию соответствующие представления величины.Только будущие исследования могут определить, требуется ли предварительная настройка по величине или числовая настройка категорий числа предлагают лучшее объяснение эффектов привязки, которые мы наблюдаемый.

Важно отметить, что, хотя предпочтительное объяснение этих результатов, Эффекты закрепления могут быть вызваны другими механизмами. Пока наши результаты кажутся несовместимыми с другими описаниями эффектов привязки, исследования явно не исключали наличие конкурирующих объяснений.Кроме того, мы, безусловно, признаем, что выборочная доступность и привязка и недостаточная корректировка счетов могут объяснить эффекты закрепления наблюдаются в других ситуациях.

4.3 Заключение

В текущих исследованиях участники явно рассматривали привязку значения перед предоставлением оценки. По общему признанию, это явное учет якорных ценностей редко встречается в повседневной жизни. Однако Кричер и Гилович (2007) продемонстрировали, что «Случайно» представленные якоря, такие как номер на майке футболиста, может влиять на оценки, такие как вероятность что игрок зарегистрирует мешок в предстоящей игре.Их выводы в сочетании с нашими результатами показывают, что случайно представленные якоря — как явно рассматриваемые якоря — могут влияние расчетов. Более того, такой эффект мог бы быть самым большим. устойчивый, когда способность (или предположительно мотивация) людей обрабатывать информация ограничена. Короче говоря, математика, выполняемая в повседневной среде, там, где времени мало, а мотивация не идеальна, может быть обычно предвзято относится к якорям, что обычно остается незамеченным.

Список литературы

Blaneknship, K.Л., Вегенер, Д. Т., Петти, Р. Э., Детвейлер-Беделл, Б., И Мэйси, К. Л. (2008). Проработка и последствия закрепленного оценки: установочный взгляд на числовую привязку. Журнал экспериментальной социальной психологии, 44, 1465–1476.

Брайсберт, М. (1995). Чтение арабских чисел: О природе числовая шкала и происхождение фонологической перекодировки. Журнал экспериментальной психологии: Общие, 124, 434–452.

Чепмен, Г. Б., и Джонсон, Э.Дж. (1999). Якорение, активация и построение ценностей. Организационное поведение и человек Процессы принятия решений, 79 , 115–153.

Чепмен, Г. Б., и Джонсон, Э. Дж. (2002). Включая нерелевантное: Якоря в суждениях веры и ценности. В Т. Гилович, Д. Гриффин и Д. Канеман (ред.), Эвристика и предубеждения: психология интуитивное суждение. (стр. 120–138) Cambridge University Press: New Йорк.

Кричер, К. Р. и Гилович, Т.(2007). Случайное окружение якоря. Журнал принятия решений в отношении поведения, 21 , 241–251.

den Heyer, K., & Briand, K. (1986) Прайминг однозначных чисел: Активация автоматического распространения рассеивается как функция семантического расстояние. Американский журнал психологии, 99, 315–339.

Englich, B., Mussweiler, T., & Strack, F. (2006). Играя в кости с уголовные приговоры: влияние нерелевантных якорей на вынесение судебных решений экспертами. Личность Бюллетень социальной психологии, 32 , 188–200.

Эпли, Н., и Гилович, Т. (2001). Возвращение регулировки в эвристика привязки и настройки: Дифференциальная обработка самопроизвольные и предоставленные экспериментатором якоря. Психологический Наука, 12 , 391–396.

Эпли, Н., и Гилович, Т. (2004). Корректировки недостаточно? Бюллетень личности и социальной психологии, 30 , 447–460.

Эпли, Н., и Гилович, Т.(2005). Когда напряженное мышление влияет осуждающая привязка: дифференциальные эффекты предупреждения и льготы на якоря, созданные самостоятельно или извне . Журнал принятия поведенческих решений, 18, , 199–212.

Эпли, Н. и Гилович, Т. (2006). Крепление и регулировка эвристика: почему корректировок недостаточно. Психологический Science, 17, 311–318.

Яковиц, К. Э. и Канеман, Д. (1995). Меры анкеровки в оценочные задачи. Бюллетень личности и социальной психологии, 21, 1161–1167.

Koechlin, E., Naccache, L., Block, E., & Dehaene, S. (1999). Грунтованный числа: Изучение модульности числовых представлений с замаскированная и немаскированная семантическая прайминг. Журнал экспериментальных исследований Психология: человеческое восприятие и производительность, 25, 1882–1905.

Mussweiler, T., & Strack, F. (1999). Проверка на соответствие гипотезам и семантическое праймирование в парадигме привязки: выборочная доступность модель. Журнал экспериментальной социальной психологии, 35 , 136–164.

Mussweiler, T., & Strack, F. (2000). Использование категории и образца знания в решении якорных задач. Журнал Личность и социальная психология, 78, 1038–1052.

Mussweiler, T., & Strack, F. (2001). Семантика привязки. Организационное поведение и процессы принятия решений людьми, 86, 234–255.

Оппенгеймер, Д. М., ЛеБёф, Р. А., и Брюэр, Н.Т. (2008). Якоря aweigh: демонстрация кросс-модального закрепления и величины грунтовка. Познание, 106 , 13–26.

Ratinckx, E., Brysbaert, M., & Fias, W. (2005). Именование двузначного арабского языка цифры: данные исследований замаскированного грунтования. Журнал Экспериментальная психология: человеческое восприятие и производительность, 31, 1150–1163.

Рейнвоет Б. и Брайсберт М. (1999). Однозначный и двузначный арабский цифры относятся к одной и той же семантической числовой строке. Познания, 72, 191–201.

Reynvoet, B., Brysbaert, M., & Fias, W. (2002). Семантическое праймирование в именование номеров. Ежеквартальный журнал экспериментальной психологии. Серия A: Экспериментальная психология человека, 55, 1127–1139.

Шварц, Н. (1994). Суждения в социальном контексте: предубеждения, недостатки, и логика разговора. В М. Занна (Ред.). Успехи в экспериментальная социальная психология (т. 26, стр. 125–162). Сан Диего: Академическая пресса.

Strack, F., & Муссвайлер, Т. (1997). Объясняя загадочную привязку Эффект: Механизмы выборочной доступности. Журнал Личность и социальная психология, 73 , 437–446.

Торстейнсон, Т. Дж., Брейер, Дж., Этвелл, А., Гамильтон, К. и Приветт, М. (2008). Эффект привязки к суждениям о производительности. Организационное поведение и процессы принятия решений людьми, 107 , 29–40.

Тверски А. и Канеман Д. (1974). Суждение в условиях неопределенности: Эвристика и предубеждения. Science, 185, , 1124–1131.

Уилсон, Т. Д., Хьюстон, К. Э., Этлинг, К. М., и Брекке, Н. (1996). А новый взгляд на эффекты привязки: базовая привязка и ее антецеденты. Journal of Experimental Psychology: General, 125 , 387–402.

Вонг, К. Ф. Э., и Квонг, Дж. Й. Ю. (2000). 7300 м равно 7,3 км? Та же семантика, но разные эффекты привязки. Организационный Поведение и процессы принятия решений людьми, 82 , 314–333.

---

Этот документ был переведен с L ^A T _E X пользователем H ^E V ^E A .

Что такое метрическая система? — [Определение, факты и пример]

Что такое метрическая система?

Метрическая система — это система измерения, в которой метр, литр и грамм используются в качестве основных единиц длины (расстояния), вместимости (объема) и веса (массы) соответственно.

Для измерения меньших или больших количеств мы используем единицы, производные от метрических единиц

• На данном рисунке показано расположение метрических единиц, которые меньше или больше базовой единицы.
• Блоки справа от базового блока меньше, чем базовый блок. Когда мы движемся вправо, каждая единица становится в 10 раз меньше или одна десятая единицы слева от нее. Итак, деци означает одну десятую базовой единицы, санти — одну десятую деци или одну сотую базовой единицы, а милли — одну десятую деци или одну тысячную. базового блока.
• Блоки слева от базового блока больше, чем базовый блок. Когда мы движемся влево, каждая единица в 10 раз больше, чем единица справа.Таким образом, «дека» означает десятикратную базовую единицу, «гекто» — это десятикратная «дека» или сто кратная базовая единица, а «килло» — это десятикратная величина «гекто» или тысяча раз больше базовой единицы.

килограммов	Hecto	Дека	Базовый блок	Деци	Сенти	Милли
1000	100	10	1	1/10	1/100	1/1000

Итак, единицы измерения длины, веса (массы) и вместимости (объема) в метрической системе:

Длина: Миллиметр (мм), Дециметр (дм), Сантиметр (см), Метр (м) и Километр (км) используются для измерения длины, ширины или высоты объекта.

Примеры включают измерение толщины или длины дебетовой карты, длины ткани или расстояния между двумя городами.

Километр (км)	Гектометр (гм)	Декаметр (плотина)	Счетчик (м)	Дециметр (дм)	Сантиметр (см)	Миллиметр (мм)
1000	100	10	1	1/10	1/100	1/1000

Вес т : Грамм (г) и килограмм (кг) используются для измерения веса объекта с помощью инструментов.

Примеры включают измерение веса фруктов или собственного веса.

Килограмм (кг)	Гектограмм (hg)	Декаграмма (даг)	Грамм (г)	Дециграмма (дг)	Сантиграмма (кг)	Миллиграмм (мг)
1000	100	10	1	1/10	1/100	1/1000

Вместимость: Миллилитр (мл) и литр (л) используются для измерения количества жидкости, которое может вместить объект.

Примеры включают измерение количества сока в банке для сока или количества воды в резервуаре для воды.

килолитров (кл)	Hecto литр (гл)	Дека литр (дал)	L итер (л)	Deci литр (дл)	Centi литр (cl)	Милли литр (мл)
1000	100	10	1	1/10	1/100	1/1000

Время: Секунда — базовая единица времени.Другие метрические единицы времени:

.

Метрические единицы преобразования: Метры, граммы и литры считаются основными единицами измерения длины, веса и объема соответственно.

Вот как мы можем умножать или делить для преобразования в метрическую систему. Чтобы преобразовать большую единицу в меньшую, мы перемещаемся влево для записи, умножаем на 10. Двигаясь справа налево, от меньшей единицы к большей, мы делим на 10.

Давайте рассмотрим несколько примеров преобразования одной единицы измерения в другую.

Пример 1. Преобразование 5 км в м.

As 1 км = 1000 м

Следовательно, 5 км = 5 × 1000 = 5000 м

Пример 2: Перевести 250 кг в миллиграммы.

Мы знаем, что 1 г = 1000 мг и 1 кг = 1000 г

Итак, сначала преобразуем кг в г как:

1 кг = 1000 г

Следовательно, 250 кг = 250 × 1000 г = 250 000 г

Теперь конвертируем g в мг:

1 г = 1000 мг, следовательно: 250 000 г = 250 000 × 1000 мг = 250 000 000 мг

Пример 3: Перевести 250 мл в литры.

1 литр = 1000 мл

Следовательно, 450 мл = 450 ÷ 1000 = 0,45 литра

Стандартные единицы США или обычная система используют общепринятые единицы.

Эта система измеряет:

• Длина или расстояние в дюймах, футах, ярдах и милях.
• Вместимость или объем в жидких унциях, чашках, пинтах, квартах или галлонах.
• Вес или масса в унциях, фунтах и ​​тоннах.

Интересные факты Тонна — это 1000 килограммов. Метрическая система берет свое начало в 1670 году математиком по имени Габриэль Мутон. С 1960-х годов метрическая система называется «Международная система единиц» или «СИ» (от французского «Système International»). Префиксы метрической системы можно запомнить с помощью мнемоники «Король Генрих умер от питья холодного молока» Есть и единицы больше килограмма. У них есть префикс мега, гига и тера.Мега — это 1000 килограммов. Гига в 1000 раз больше мега, а тера — в 1000 раз больше гига.

Давайте споем!

Найдите миллиметр в кончике карандаша,

Найдите сантиметр в большой скрепке.

Найдите миллилитр в соке, который вы пьете,

Найдите литр воды в раковине.

Найдите грамм манго, которое вы съели,

Найди килограмм в восьмерке!

Давайте сделаем это!

Вместо того, чтобы передавать вашему ребенку наши рабочие листы с задачами со словами, найдите примеры из реальной жизни, в которых ребенок должен измерить длину, вес или вместимость в метрических единицах или преобразовать большие единицы в меньшие.Например, в продуктовом магазине попросите ребенка взвесить 8 яблок с помощью цифровых весов в килограммах. Затем попросите его перевести вес в граммы и миллиграммы.

Сопутствующий математический словарь

Вариационные уравнения | Purplemath

Purplemath

Проблемы с вариациями несложны, если вы освоите жаргон.Единственная реальная трудность — это выучить несколько специализированный словарный запас и методы этой классификации проблем.

Проблемы вариации включают довольно простые отношения или формулы, в которых одна переменная равна одному члену. Этот термин может быть линейным (что-то с просто « x »), квадратичным (что-то в « x ² »), более чем одной переменной (например, « r ² h ») , квадратный корень (что-то вроде «

«) или что-то еще.

Но в формуле всегда есть только один член; этот член будет умножен на некоторое число, и, если вы еще не знаете, что это за число, это число обычно обозначается как « k ». Это число k называется «постоянной вариации».

MathHelp.com

Итак, вариационные уравнения могут иметь сложные выражения, но в них всегда будет только один член.В их уравнениях никогда не будет двух или более членов, сложенных вместе. Например, y = 3 x является уравнением вариации, а y = 3 x + 2 — нет.

Примером вариационного уравнения может быть формула для площади круга:

На языке вариантов:

площадь A напрямую зависит от квадрата радиуса r

…и постоянная изменения равна k = π. Эта формула является примером «прямого» изменения. «Прямое изменение» означает, что в одном члене формулы переменная находится «сверху».

(Кстати, если вы видите формулу со знаком «∝» вместо знака «равно», этот символ произносится как «прямо пропорционален» и указывает на то, что они дали вам прямой- уравнение вариации, но без указания постоянной вариации.)

С другой стороны, «обратная вариация» означает, что переменная находится внизу, внизу дроби.Предположим, например, что вы унаследовали счет денежного рынка, содержащий 100 000 долларов, и задаетесь вопросом, сколько денег ваш богатый дядя изначально вложил восемь лет назад. В зависимости от средней процентной ставки « r » формула, которую вы использовали бы, будет выглядеть так:

… где P — это основная сумма, которую вложил ваш дядя. (Кстати, эта формула является вариантом формулы сложных процентов.) На языке вариаций эта формула читается как:

основной P изменяется обратно пропорционально

…с постоянной вариации k = 100000.

Другой вариант вариации — «совместно». «Совместная вариация» означает «напрямую, но с двумя или более переменными». Примером может служить формула для площади треугольника с основанием « b » и высотой « h »:

Прописью:

площадь A изменяется вместе с b и h

Константа вариации для этого уравнения равна

k = ¹ / ₂ .

На рассмотрение:

• «F изменяется как x » означает F = kx

• «F одновременно меняется как x и y » означает F = kxy

• «F изменяется как x + y » означает F = k ( x + y )

• «F изменяется обратно пропорционально, так как x » означает

Будьте осторожны с этими двумя средними утверждениями выше.Почти всегда, когда вы переводите словесные задачи с английского на математику, «и» означает «плюс» или «добавлено к». Но в совместном варианте «и» просто означает, что «оба вместе находятся на одной стороне дроби» (обычно наверху), и вы умножаетесь. Если вы должны добавить две переменные, они будут использовать формат из этого третьего маркированного примера выше, или они скажут «варьируется как сумма x и y .

(Если они заставляют вас работать с чем-то, что «прямо» меняется с одним и «обратно» с другим, это можно назвать «комбинированным» вариантом.)

---

Перевод проблем с вариациями не так уж и плох, если вы освоите его. Но затем они хотят, чтобы вы перешли к настройке и решению текстовых задач. Обычно они делятся на две категории: те, где они хотят, чтобы вы нашли значение « k », и те, где они хотят, чтобы вы нашли какое-то другое значение, но только после того, как вы сначала нашли « k ». . Вот несколько примеров:

• Если

  y изменяется прямо как x ² и y = 8, когда x = 2, найдите y , когда x = 1.

Так как это прямая вариация, формула: « y = kx ² ». Причина, по которой мне дали точку данных ( x , y ) = (2, 8), заключается в том, что Мне нужно найти значение « к ». Я вставляю информацию, которую они мне дали, и решаю для k :

y = k x ²

8 = к (2 ² )

8 = 4 к

2 = к

Теперь, когда у меня есть k , я могу полностью переписать формулу:

Этим я могу ответить на вопрос, который они на самом деле задали: «Найдите y , когда x = 1.«

y = 2 x ²

y = 2 (1) ²

y = 2 (1)

y = 2

Тогда ответ:

---

• Если

  y изменяется вместе как x и z , и y = 5, когда x = 3 и z = 4, то найдите y , когда x = 2 и z = 3.

Переводя формулу с английского на математические, получаю:

Вставив точку данных, которую они мне дали, и решив значение k , я получил:

5 = к (3) (4)

5 = 12 к

⁵ / ₁₂ = к

Теперь, когда у меня есть значение k , я могу вставить новые значения и найти новое значение y :

y = ( ⁵ / ₁₂ ) xz

y = ( ⁵ / ₁₂ ) (2) (3)

y = ( ⁵ / ₁₂ ) (6)

y = ⁵ / ₂

Тогда ответ:

---

• Учитывая, что

  y изменяется обратно пропорционально квадрату разницы w и x , и что y = 6, когда w = 3 и x = 1, найдите уравнение для y .

Это довольно сложно. Я буду работать небольшими частями.

Мне сказали, что y изменяется обратно пропорционально указанному выражению, поэтому я знаю, что форма выражения будет иметь постоянную вариации поверх рационального выражения (то есть полиномиальную дробь) и переменную выражение в нижней части этого выражения.Но что такое переменное выражение?

«Разница между w и x » означает:

Квадрат этой разницы:

Это выражение будет внизу дроби, а постоянная вариации k будет вверху, так что мое уравнение на данный момент:

Чтобы найти полное уравнение для y , мне нужно найти значение константы.Для этого я вставлю значения, которые они мне дали:

6 = к / (3 — 1) ²

6 = к / (2) ²

6 = к /4

24 = к

Теперь у меня есть все части моего уравнения, и мой ответ:

---

URL: https: // www.purplemath.com/modules/variatn.htm

12. Численное решение по Рунге-Кутта (RK4) для дифференциальных уравнений

В последнем разделе метод Эйлера дал нам один из возможных подходов к численному решению дифференциальных уравнений.

Проблема с методом Эйлера заключается в том, что для получения достаточно точного результата необходимо использовать небольшой размер интервала. То есть это не очень эффективно.

Метод Рунге-Кутта дает лучший результат за меньшее количество шагов.

Метод Рунге-Кутты Порядок 4 Формула

Заявления РК4

Механика

Биология

• Хищник-жертва модели
• Обвал рыболовства
• Доставка лекарств
• Предсказание эпидемии

Физика

• Модели изменения климата
• Защита от озона

Авиация

• Бортовые компьютеры
• Аэродинамика

`y (x + h)` = y (x) + `1/6 (F_1 + 2F_2 + 2F_3 + F_4)`

где

`F_1 = hf (x, y)`

`F_2 = hf (x + h / 2, y + F_1 / 2)`

`F_3 = hf (x + h / 2, y + F_2 / 2)`

`F_4 = hf (x + h, y + F_3)`

Откуда взялась эта формула?

Вот краткая предыстория формулы.

Вывод формулы

Ранее мы узнали, что ряд Тейлора дает нам достаточно хорошее приближение к функции, особенно если мы достаточно близки к некоторой известной начальной точке и берем достаточно членов.

Однако одним из недостатков метода Тейлора является то, что вам нужно дифференцировать функцию один раз для каждого нового члена, который вы хотите вычислить. Это может быть проблематично для сложных функций и плохо работает при компьютерном моделировании.

Карл Рунге (произносится как «рунга») и Вильгельм Кутта (произносится как «коота») стремились предоставить метод приближения функции без необходимости дифференцировать исходное уравнение.

Их подход заключался в моделировании как можно большего количества шагов метода рядов Тейлора, но с использованием оценки только исходной функции.

Метод заказа 2 Рунге-Кутты

Начнем с двух вычислений функции вида:

`F_1 = hf (x, y)`

`F_2 = hf (x + alpha h, y + beta F_1)`

«Альфа» и «бета» — неизвестные величины. Идея заключалась в том, чтобы взять линейную комбинацию членов `F_1` и` F_2`, чтобы получить приближение для значения `y` при` x = x_0 + h` и найти подходящие значения `alpha` и` beta`. .

Путем сравнения значений, полученных с использованием метода рядов Тейлора и приведенных выше терминов (я избавлю вас от подробностей здесь), они получили следующее: Метод Рунге-Кутты Порядка 2 :

`y (x + h) = y (x) +1/2 (F_1 + F_2)`

где

`F_1 = hf (x, y)`

`F_2 = hf (x + h, y + F_1)`

Метод заказа Рунге-Кутты 3

Как обычно в этой работе, чем больше терминов мы возьмем, тем лучше будет решение.На практике решение порядка 2 используется редко, поскольку оно не очень точное.

Лучший результат дает метод Порядка 3:

`y (x + h) =` y (x) +1/9 (2F_1 + 3F_2 + 4F_3) `

где

`F_1 = hf (x, y)`

`F_2 = hf (x + h / 2, y + F_1 / 2)`

`F_3 = hf (x + (3h) / 4, y + (3F_2) / 4)`

Это было получено аналогично предыдущей формуле путем сравнения результатов ряда Тейлора.

Наиболее часто используемая формула Рунге-Кутта — это формула четвертого порядка (RK4), поскольку она дает лучший компромисс между вычислительными требованиями и точностью.(0,1 + 0,96545654732)) « = -0,03154393258`

Шаг 2

Затем мы берем эти 4 значения и подставляем их в формулу Рунге-Кутты RK4:

`y (x + h)` = y (x) +1/6 (F_1 + 2F_2 + 2F_3 + F_4) `

`= 1 + 1/6 (-0.03678794411« — \ 2xx0.03454223937« — \ 2 xx0.03454345267« {: — \ 0.03154393258)`

`= 0,9655827899`

Используя это новое значение `y`, мы начинаем заново, находя новые` F_1`, `F_2`,` F_3` и `F_4`, и подставляем их в формулу Рунге-Кутты.

Мы продолжаем этот процесс и составляем следующую таблицу значений Рунге-Кутты. (Я использовал электронную таблицу для получения таблицы. Использование калькулятора очень утомительно и подвержено ошибкам.)

`x`	`г`	`F_1 = h dy / dx`	` x + h / 2`	`y + F_1 / 2`	`F_2`	`y + F_2 / 2`	`F_3`	`x + h`	`y + F_3`	`F_4`
0	1	−0.0367879441	0,05	0,9816060279	-0,0345422394	0,9827288803	-0,0345434527	0,1	0,9654565473	-0,0315439326
0,1	0,9655827899	-0,0315443	0,15	0,9498106398	-0,0278769283	0,9516443257	−0.0278867954	0,2	0,9376959945	-0,023647342
0,2	0,937796275	-0,023648185	0,25	0,	21824	-0,018	61	0,9283328869	-0,0189548088	0,3	0,14662	-0,0138576597
0,3	0.918 59	-0,0138588628	0,35	0,	86745	-0,0084782396	0, 89861	-0,0085314167	0,4	0,

66892 -0,0029773028 0,4 0,21929 -0,0029786344 0,45 0,28756 0,0026604329 0.24093 0,002580704 0,5 0,

28969 0,0082022376 0,5 0,

9839 0,0082010354 0,55 0,03567 0,013727301 0,34895 0,0136258867 0,6 0,57257 0,018973147 0.6 0,65986 0,0189722976 0,65 0,9361

4 0,0240794197 0,9387463085 0,0239658709 0,7 0,9506724696 0,0287752146 0,7 0,9506796142 0,0287748718 0,75 0,9650670501 0,0332448616 0.967302045 0,0331305132 0,8 0,9838101274 0,0372312889 0,8 0,9838057659 0,0372315245 0,85 1,0024215282 0,0409408747 1,0042762033 0,0408359751 0,9 1.024641741 0,0441484563 0.9 1.024628046 0,04414 0,95 1.0467026764 0,0470593807 1.0481577363 0,0469712279 1 1.07159 0,04947 1 1.0715783953

Я не включил никаких значений после `y` в нижнюю строку, поскольку мы не будем их использовать.

Вот график найденных нами решений от «x = 0» до «x = 1».

Для интереса я расширил результат до `x = 10`, и вот получившийся график:

Упражнение

Решите следующее, используя RK4 (Метод Рунге-Кутты порядка 4) для `0 le x le 2`. Используйте размер шага h = 0,2:

`dy / dx = (x + y) sin xy`

`y (0) = 5`

Ответ

Шаг 1

У нас есть x_0 = 0 и y_0 = 5.

`F_1 = hf (x, y)` `= 0,2 ((0 + 5) sin (0) (5))` = 0`

Для `F_2` нам нужно знать:

`x + h / 2 = 0 + 0,2 / 2 = 0,1` и

`y + F_1 / 2 = 5 + 0/2 = 5`

Подставляем их в выражение `F_2`:

`F_2 = hf (x + h / 2, y + F_1 / 2)` = 0,2 ((0,1 + 5) sin (0,1) (5)) `= 0,48

4937`

Для `F_3` нам нужно знать:

`y + F_2 / 2` = 5 + 0,48

4937 / 2` = 5,24450702469`

Так

`F_3 = hf (x + h / 2, y + F_2 / 2)`

`= 0.2 ((0,1 + 5,24450702469) `{: xxsin (0,1) (5,24450702469))`

`= 0,53523

2`

Для `F_4` нам нужно знать:

`y + F_3« = 5 + 0.53523

2` `= 5.53523

2`

Так

`F_4 = hf (x + h, y + F_3)`

`= 0,2 ((0,2 + 5,53523

2)` {: xxsin (0,2) (5,53523

2)) `

`= 1.02589

1`

Шаг 2

Затем мы берем эти 4 значения и подставляем их в формулу Рунге-Кутты RK4:

`y (x + h) = y (x) +1/6 (F_1 + 2F_2 + 2F_3 + F_4)`

`= 5 + 1/6 (0+` `2xx0.48

4937+ « 2xx0.53523

2 » {: + 1.02589

1) `

`= 5.5124008953`

Как и раньше, нам нужно взять это значение `y_1` и использовать новое значение` x_1 = 0,2`, чтобы найти следующее значение, `y_2`, и так далее до` x = 2`.

Ниже приводится таблица результирующих значений.

Вот и получилась таблица значений.

Посмотреть таблицу

781556634

`x`	`г`	`F_1 = h dy / dx`	` x + h / 2`	`y + F_1 / 2`	`F_2`	`y + F_2 / 2`	`F_3`	`x + h`	`y + F_3`	`F_4`
0	5	0	0.1	5	0,48 494	5.2445070247	0,53523	0,2	5,53523	1.02589
0,2	5.5124008953	1.0194689011	0,3	6.0221353458	1,229424454	6,1271131223	1,2397613573	0,4	6.7521622525	0,6102193187
0,4	6.6070775356	0,670350862	0,5	6.9422529666	-0,4816655538	6.3662447588	-0,0570142602	0,6	6.5500632755	-1,0142481364
0,6	6.3702013853	-0,8771352065	0.7	5.931633782	-1,1235642458	5.80841	-1,03 691	0,8	5,3311976162	-1,1055304726
0,8	5,31804	-1,0980514561	0,9	4,7698753724	-1,0356506358	4,80 10757825	-1,0539783626	1	4.264	-0,9493143311
1	4,2811304698	-0,9595184486	1,1	3,8013712455	-0,8453508288	3.8584550553	-0,8850171765	1,2	3,3961132933	-0,73891
1,2	3,421268202	-0,75	1.3	3,0416593442	-0,6304549629	3.1060407205	-0,6882207337	1,4	2,7330474682	-0,5227646767
1,4	2,7680459044	-0,5581856458	1,5	2.4889530815	-0,4450766109	2,5455075989	-0,5066587622	1.6	2,2613871422	-0,354308929
1,6	2.2987183509	-0,3984550218	1,7	2,09949084	-0,3150804545	2,1411781236	-0,3672394563	1,8	1,9314788946	-0,2454079264
1,8	1.9639678892	-0.2886730166	1,9	1,8196313809	-0,230980612	1,8484775833	-0,2714612259	2	1.6	-0,1779964411
2	1,71870

Еще раз, я не включил никаких значений после `y` в нижнюю строку, поскольку они не требуются.

Вот график найденных нами решений от «x = 0» до «x = 2».

Для интереса я расширил результат до `x = 6`, и вот получившийся график:

Заметим, что график не очень плавный. Если мы используем меньшее значение h, кривая в целом будет более гладкой.

Фактически, эта кривая является асимптотической по отношению к оси «x» (она плавно приближается к оси по мере увеличения «x»). На приведенном выше графике показано, что происходит, когда наши интервалы слишком грубые.(Этих движений после примерно `x> 4.5` не должно быть.)

Вот снова график решения, но на этот раз я использовал «h = 0,1». Это лучше, но все же есть «покачивание» около x = 5, которого не должно быть.

Если бы я взял еще меньшие значения `h`, я бы получил более плавную кривую. Однако это только до определенного момента, потому что со временем ошибки округления становятся значительными. Кроме того, время вычислений увеличивается без особой пользы.

Улучшения Рунге-Кутта

Как вы можете видеть из приведенного выше примера, на кривой есть точки, где значения `y` меняются относительно быстро (между` 0` и `1`), и другие места, где кривая более близка к линейной (от` 1` до `2`).Кроме того, у нас странное поведение около x = 5.

На практике, при написании компьютерной программы для выполнения Рунге-Кутты, мы допускаем переменные значения «h» — довольно маленькие, когда кривая изменяется быстро, и большие значения «h», когда кривая относительно гладкая.

Системы компьютерной алгебры Mathematics (такие как Mathcad, Mathematica и Maple) включают в себя процедуры, которые вычисляют RK4 за нас, поэтому нам просто нужно указать функцию и интересующий интервал.

Осторожно

Всегда будьте осторожны со своими ответами! Численные решения — это только приближения, и при определенных условиях вы можете получить хаотические результаты.

Нужна помощь в решении другой задачи с исчислением? Попробуйте решить проблемы.

Заявление об ограничении ответственности: IntMath.com не гарантирует точность результатов. Решение проблем, предоставленное Mathway.

Закажите одного из наших репетиторов Лиги плюща, который поможет вам овладеть математикой и улучшить свои оценки.

Образование: Компьютерные науки и математика, Стэнфордский университет

Предметы: Алгебра, геометрия, триггер, исчисление, Adv.Исчисление, подготовка к SAT / ACT

Биография: Привет! Я Лигия, мне очень нравится наставлять других, и я работала репетитором математики в Стэнфорде. Я также интересуюсь физическими науками, и я провожу исследования с использованием машинного обучения в биологических проблемах. Я люблю теннис, бразильскую музыку и все виды рукоделия.

Скорость: 100 $ / час

.